1、计算题 一小汽车从静止开始以2 m/s2的加速度行驶时，恰有一自行车以6 m/s的速度从车旁匀速试过。
⑴ 汽车追上自行车之前经多长时间两者相距最远？此距离是多少？
⑵ 何时追上自行车，追上时汽车的速度是多少？
参考答案：（1）3s? 9m（2）6s? 12m/s
本题解析：设两者相距为
，根据题意则
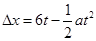，这是一元二次方程，所以当t=3s有最大值，距离为9m；
当为零时相遇，所以t=6s（t=0s舍弃），所以汽车速度为v=at=12m/s
点评：此类题型考察了匀变速直线运动规律，将已知量代入相关公式即可，通过数学一元二次函数的知识，便能求出最大值，以及何时相遇。
本题难度：一般
2、简答题 一辆汽车从静止开始匀加速直线开出，然后保持匀速运动，最后匀减速直线运动，直到停止，下表给出了不同时刻汽车的速度大小：
| 时刻/s | 1.0 | 2.0 | 3.0 | 5.0 | 7.0 | 9.5 | 10.5
速度/m?s-1
3
6
9
12
12
9
3
|
试求：（1）汽车做匀速运动时的速度大小是否为12m/s？汽车做加速运动时的加速度和减速运动时的加速度大小是否相等？
（2）汽车从开出到停止总共经历的时间是多少？
（3）汽车通过的总路程是多少？
参考答案：（1）汽车匀速运动的速度大小是12m/s．
根据匀加速运动的加速度知，4s末速度为12m/s，根据匀减速直线运动的加速度知9s末的速度为12m/s．在4～9s内做匀速直线运动．
3.0s前汽车做匀加速直线运动，9.5s后做匀减速直线运动．
a1=△v△t=3m/s2
a2=△v△t=-6m/s2
汽车做加速运动时的加速度和减速运动时的加速度大小不相等．
（2）对9.5s后分析，需再经△t停下．
△t=△va=0-9-6s=1.5s
运动时间t共=9.5+△t=11s
故汽车从开出到停止共经历的时间是11s．
（3）前4s内的位移x1=12a1t12=12×3×16m=24m
在4～9s内的位移x2=vt2=12×5m=60m
在9～11s内的位移x3=v2t3=6×2m=12m
所以总路程s=x1+x2+x3=96m
故汽车通过的总路程是96m．
答：（1）汽车做匀速运动时的速度大小是12m/s，
汽车做加速运动时的加速度和减速运动时的加速度大小是相等．
（2）汽车从开出到停止总共经历的时间是11s
（3）汽车通过的总路程是96m．
本题解析：
本题难度：一般
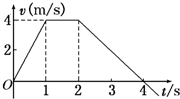
3、选择题 如图所示为某质点运动的速度图象，由图象得到的正确结果是（ ）
A．0～1s内的平均速度是4m/s
B．0～2s内的位移大小是6m
C．0～1s内的加速度小于2～4s内的加速度
D．0～2s内质点做匀变速直线运动
考试问吧
