1、选择题  两球a和b的质量分别为ma和mb、直径分别为da和db（da>db）。将a、b球依次放入一竖直放置、内径为d（da＜d＜da十db）的平底圆筒内，如图所示。设a、b两球静止时对圆筒侧面的压力大小分别为f1和f2，筒底所受的压力大小为F。已知重力加速度大小为g。若所有接触面都是光滑的，则

[? ]
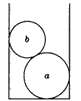
A．F=(ma+mb)g，f1=f2
B．F=(ma+mb)g，f1≠f2
C．mag＜F＜(ma+mb)g，f1=f2
D．mag＜F＜(ma+mb)g，f1≠f2

参考答案：A

本题解析：

本题难度：一般

2、选择题  一根弹簧受到30N的拉力时，长度为20cm，受到30N的压力时，长度为14cm，则该弹簧的原长L和劲度系数k分别为
A.L= 17cm k=1000N/m
B.L= 10cm k=1.5N/m
C.L= 17cm k=" 10" N/m
D.L= 10cm k=150N/m

参考答案：A

本题解析：试题分析：设弹簧的原长为L0，根据胡克定律有：F1=k（L1-L0），F2=k（L0-L2）．代入数据有：30=k（0.2-L0），30=k（L0-0.14），联立两式得，k=1000N/m，L0=0.17m=17cm，A正确。
考点：本题考查了胡克定律。

本题难度：困难

3、计算题  如图所示，A、B的重力分别为4.6N和8N，各接触面间的动摩擦因数均为0.2，连接墙壁与A之间的细绳与水平方向夹角为37°，现从A下方匀速拉出B。求：
（1）这时系A的绳中的张力大小为多少？
（2）所需的水平拉力F为多少？（sin37°=0.6，cos37°=0.8，要求要分别画出A、B物体的受力图）

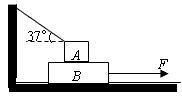
参考答案：（1）T=1N
（2）F=3.2N，图“略”

本题解析：

本题难度：一般

4、计算题  (10分)如图所示，匀强电场的电场强度为E，一带电小球质量为m，轻质悬线长为l，静止时悬线与竖直方向成30°角．

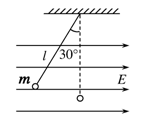
(1)小球带何种电荷，电荷量是多少？
(2)若将小球拉到悬点正下方由静止释放，小球通过原平衡位置时的速度大小是多少？

参考答案：(1) q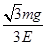＝?(2)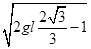

本题解析：(1)小球静止时，其受力如图所示，小球所受电场力的方向与场强方向相反，所以小球带负电．由平衡条件得Eq＝mgtanθ，q＝.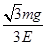
(2)设小球通过原平衡位置时的速度大小为v，由动能定理Eqlsin30°－mgl(1－cos30°)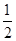＝mv2，由以上两式可解得
v＝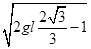
本题考查了带电粒子在电场中的平衡问题和动能定理的应用，先进行受力分析，根据力的合成而后分解进行求解，若将小球拉到悬点正下方由静止释放，到达最低点过程中只有重力和电场力做功，可由动能定理求解
点评：电场力和重力都是保守力，做功的大小与路径无关，只与初末位置有关，所以在求这两个力做功的过程中不需要考虑中间的运动过程，只需要确定初末状态即可

本题难度：一般

5、简答题  如图所示，在光滑的水平地面上，有一质量为mA=2.0kg的长木板，以v0=14m/s的速度向右运动．若再在A板右端轻放一个带正电荷电荷量为0.20C、质量为0.10kg的物块B，A、B处在B=0.50T的匀强磁场中，A、B间动摩擦因数为μ，相互绝缘，A板足够长，g取10m/s2．试求：
（1）B物块的最大速度；
（2）A板的最小速度；
（3）此过程中A、B系统增加的总内能．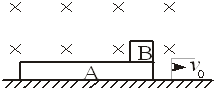

参考答案：（1）当物块B所受到的竖直向上的洛伦兹力和重力相等时，B对A的压力为零，此时B获得最大速度，则有：
? qvmB=mBg? 解得：vm=10 m/s
（2）对A、B物体系统水平方向不受外力，所以系统的动量守恒．当B的速度最大时，B对A没有压力，A的速度最小．规定木板A的初速度方向为正方向．则根据动量守恒定律得：
? mAv0=mAvA+mBvm，
代入解得，A板的最小速度vA=13.5m/s．
（3）根据能量守恒定律得，此过程中A、B系统增加的总内能等于机械能的减小，即有：
△E=12mAv20-12mAv2A+12mBv2m
代入解得，△E=8.75J
答：
（1）B物块的最大速度为10m/s；
（2）A板的最小速度为13.5m/s；
（3）此过程中A、B系统增加的总内能为8.75J．

本题解析：

本题难度：一般