1、选择题  水平桌面上质量为1kg的物体受到2N的水平拉力，产生1.5m/s2的加速度。若水平拉力增至4N，则物体将获得的加速度为（?）
A．2.5 m/s2
B．3.5 m/s2
C．4m/s2
D．3 m/s2

参考答案：B

本题解析：分析物体的受力，根据牛顿第二定律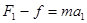：，2-f=1.5×1，解得f=0.5N
当力增加至4N时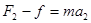：，代入数据，解得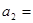3.5 m/s2
所以选B。

本题难度：简单

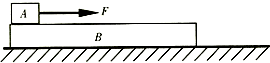
2、简答题  如图所示，一质量M=3.0kg、足够长的木板B放在光滑的水平面上，其上表面放置质量m=l.0kg的小木块A，A、B均处于静止状态，A与B间的动摩擦因数?=0.30，且最大静摩擦力与滑动摩擦力大小相等．现给木块A施加一随时间t变化的水平力F=kt（k=2.0N/s），取g=10m/s2．
（1）若木板B固定，则经过多少时间木块A开始滑动？
（2）若木板B固定，求t2=2.0s时木块A的加速度大小．
（3）若木板B不固定，求t3=1.0S时木块A受到的摩擦力大小．

参考答案：（1）当木板固定时，A开始滑动瞬间，水平力F与最大静摩擦力大小相等，则：
F=f=μmg
设经过t1时间A开始滑动，则：F=kt1
t1=μmgk=0.3×1×102s=1.5s
（2）t=2s时，有：
F=kt=2×2N=4N
有牛顿第二定律有：F-μmg=ma
a=F-μmgm=4-0.3×1×101m/s2=1m/s2
（3）在t=1s时水平外力为：F=kt=2×1N=2n
由于此时外力小于最大静摩擦力，两者一定不发生相对滑动，故一起做匀加速运动，以整体为研究对象，有牛顿第二定律可得：
F=（m+M）a′
a′=FM+m=21+3m/s2=0.5m/s2
对A受力分析为：F-f=ma′
f=F-ma′=2-1×0.5N=1.5N
答：（1）若木板B固定，则经过1.5s木块A开始滑动
（2）若木板B固定，求t2=2.0s时木块A的加速度大小为1m/s2．
（3）若木板B不固定，求t3=1.0S时木块A受到的摩擦力大小为1.5N．

本题解析：

本题难度：一般

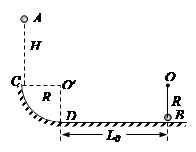
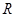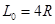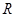3、计算题  （18分）如图所示，半径为的 1/4光滑圆弧轨道最低点D与水平面相切，在D点右侧处用长为的细绳将质量为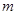的小球B（可视为质点）悬挂于O点，小球B的下端恰好与水平面接触，质量为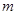的小球A（可视为质点）自圆弧轨道C的正上方H高处由静止释放，恰好从圆弧轨道的C点切入圆弧轨道，已知小球A与水平面间的动摩擦因数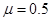,细绳的最大张力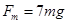,重力加速度为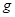，试求：
?
（1）若，小球A到达圆弧轨道最低点D时所受轨道的支持力；
（2）试讨论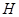在什么范围内，小球A与B发生弹性碰撞后细绳始终处于拉直状态。

参考答案：（1），方向竖直向上。（2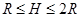）和

本题解析：
试题分析: （1）设小球运动到D点的速度为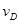
对小球在从静止上落到D点时，由机械能守恒定律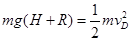：?①
在D点由牛顿第二定律：?②
由①②得，方向竖直向上。
（2）设A与B碰前速度为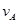，碰后A的速度为，B的速度为，
则A与B碰撞过程有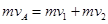：?③
弹性碰撞满足机械能守恒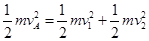：?④
由③④得A、B在碰撞过程中会发生速度交换。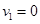，?⑤
A在由静止到碰撞前过程由动能定理有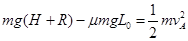：?⑥
若碰后B能在竖直平面内做完整的圆周运动，则细绳始终处于拉直状态，设小球B在最高处速度为，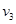
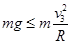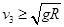则在最高处有：，得?⑦
小球B在最低点时细绳受力最大，则有?⑧
小球B从最低点到最高点由动能定理有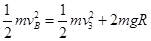：?⑨
联立①④⑤⑥⑦⑧⑨解得：?⑩
若A与B碰后B摆动的最大高度小于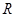，则细绳也始终处于拉直状态，
则根据机械能守恒有：?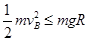
要保证A与B能发生碰撞，则?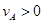
联立①④⑤⑥?解得：?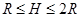
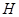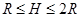故小球A与B发生弹性碰撞后细绳始终处于拉直状态的范围：和

本题难度：一般

4、选择题  如图所示，一个质量为65kg的消防员沿杆匀速下滑，在竖直方向消防员的受力情况是（　　）
A．他受到竖直向下的重力为65N
B．他受到竖直向下的重力为6.5N
C．他受到竖直向上的摩擦力为650N
D．他受到竖直向下的摩擦力为650N