1、计算题 如图所示,质量分别为m和M的两物体P和Q叠放在倾角为θ的斜面上,P、Q之间的动摩擦因数为μ1,Q与斜面间的动摩擦因数为μ2(μ1>μ2).当它们从静止开始沿斜面滑下时,两物体始终保持相对静止,则物体P受来源:91考试网 91exam.org到的摩擦力大小为多少?

参考答案:解:先取PQ为一整体,受力分析如图所示
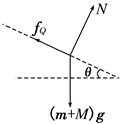
由牛顿第二定律得:(M+m)gsinθ-fQ=(M+m)a
fQ=μ2N
N=(m+M)gcosθ
以上三式联立可得a=gsinθ-μ2gcosθ
再隔离P物体,设P受到的静摩擦力为fP,方向沿斜面向上
对P再应用牛顿第二定律得:mgsinθ-fP=ma
可得出fP=μ2mgcosθ
本题解析:
本题难度:一般
2、计算题 (10分)质量M=9kg、长L=1m的木板在动摩擦因数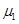 =0.1的水平地面上向右滑行,当速度
=0.1的水平地面上向右滑行,当速度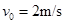 时,在木板的右端轻放一质量m=1kg的小物块如图所示.当小物块刚好滑到木板左端时,物块和木板达到共同速度.取g=10m/s2
时,在木板的右端轻放一质量m=1kg的小物块如图所示.当小物块刚好滑到木板左端时,物块和木板达到共同速度.取g=10m/s2

求:
(1)从木块放到木板上到它们达到相同速度所用的时间t;
(2)小物块与木板间的动摩擦因数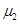 .
.
参考答案:(1)t=1s(2)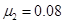
本题解析:(1)设木板在时间t内的位移为x1;木块的加速度大小为a2,时间t内的位移为x2
?则有x1= v0t-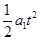 ?①
?①
x2=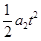 ?②
?②
x1=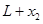 ?③
?③
又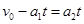 ?④
?④
你入数据得t=1s?⑤
(2)根据牛顿第二定律,有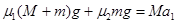 ?⑥
?⑥
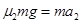 ?⑦
?⑦
解得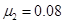 ?⑧
?⑧
评分标准:本题共10分,③⑥每式2分,其余每式1分
点评:本题难度较小,明确两物体的位移关系,由运动学规律求解
本题难度:一般
3、简答题 如图甲所示,一个足够长的“L”形金属导轨NMPQ固定在水平面内,MN、PQ两导轨间的宽度为L=0.50m.一根质量为m=0.50kg的均匀金属导体棒ab横跨在导轨上且接触良好.abMP恰好围成一个正方形.该轨道平面处在磁感强度大小可以调节的竖直向上的匀强磁场中.ab棒与导轨间的最大静摩擦力和滑动摩擦力均为fm=1.0N,ab棒的电阻为R=O.10Ω.其他各部分电阻均不计.开始时磁感强度B0=0.50T.
(1)若从某时刻(t=O)开始,调节磁感强度的大小使其以△B/△t=0.20T/s的变化率均匀增加.求经过多长时间ab棒开始滑动?此时通过ab棒的电流大小和方向如何?
(2)若保持磁感强度B0的大小不变.从t=0时刻开始,给ab棒施加一个水平向右的拉力,使它以a=4.0m/s2的加速度匀加速运动.推导出此拉力T的大小随时间变化的函数表达式.并在图乙所示的坐标图上作出拉力T随时间t变化的T-t图线.
参考答案:
(1)当棒ab所受的安培力等于最大静摩擦力时,棒刚开始运动,则有
? fm=F=ILB?①
?B=B0+△B△tt?②
?根据法拉第电磁感应定律得:E=△Φ△t=L2?△B△t?②
? I=ER?④
联立①~④解得?t=17.8s,
此时通过ab棒的电流大小为I=0.5A,由楞次定律判断可知,I的方向b→a.
(2)根据牛顿第二定律得:T-FA-f=ma?
其中安培力FA=B0IL,I=B0LvR,v=at
得FA=B20L2atR
∴T=B20L2atR+ma+f?
代入解得 T=(3+2.5t)N?
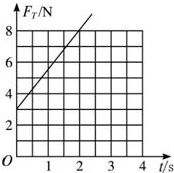
作出T-t图象如图所示.
答:
(1)经过17.8s时间ab棒开始滑动,此时通过ab棒的电流大小为0.5A,方向b→a.
(2)拉力T的大小随时间变化的函数表达式为T=(3+2.5t)N,作出T-t图象如图所示.
本题解析:
本题难度:一般
4、选择题 如图所示,质量为M的长平板车放在光滑的倾角为α的斜面上,车上站着一质量为m的人,若要平板车静止在斜面上,车上的人应当(?)
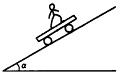
A.匀速向下奔跑
B.以加速度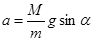 向下加速奔跑
向下加速奔跑
C.以加速度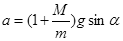 向下加速奔跑
向下加速奔跑
D.以加速度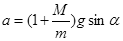 向上加速奔跑
向上加速奔跑
参考答案:C
本题解析:平板车静止在斜面上,则人对车的作用力F应沿斜面向上和平板车所受重力沿斜面向下的分力大小相等即:F=Mgsinα,
根据牛顿第三定律,则平板车对人的作用力沿斜面向下,大小为Mgsinα,
则人所受的合力F合=mgsinα+Mgsinα,沿斜面向下,
根据牛顿第二定律,人的加速度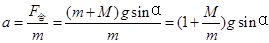 ,沿斜面向下,
,沿斜面向下,
则人应以加速度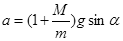 向下加速奔跑,C正确。
向下加速奔跑,C正确。
本题难度:一般
5、选择题 如图所示,一个质量为65kg的消防员沿杆匀速下滑,在竖直方向消防员的受力情况是( )
A.他受到竖直向下的重力为65N
B.他受到竖直向下的重力为6.5N
C.他受到竖直向上的摩擦力为650N
D.他受到竖直向下的摩擦力为650N
