1、选择题  将物体以60J的初动能竖直向上抛出，当它上升至某点P时，动能减为10J，机械能损失10J，若空气阻力大小不变，那么物体落回抛出点的动能为（　　）
A．36J
B．40J
C．48J
D．50J

参考答案：设物体的重力大小为G，空气阻力大小为f，抛出点到P点的高度为h，抛出点到最高点的高度为H．
从抛出点到P点过程，
根据动能定理得：-Gh-fh=△Ek=10J-60J=-50J? ①
由功能关系得：-fh=△E=-10J? ②
由上两式得到：f：G=1：4
从抛出点到最高点过程，
根据动能定理得：-GH-fH=△Ek=-60J=-60J?
将f：G=1：4代入得到
-4fH-fH=-60J
有fH=12J
则物体从抛出到落回抛出点的整个过程中，物体克服空气阻力做功为2fH=24J，机械能总损失为24J，所以
物体落回抛出点的动能为60J-24J=36J．
故选A

本题解析：

本题难度：一般

2、选择题  （选考题）如图所示，一个长为L，质量为M的长方形木板，静止在光滑水平面上，一个质量为m的物块（可视为质点），以水平初速度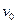，从木板的左端滑向另一端，设物块与木板间的动摩擦因数为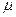，当物块与木板达到相对静止时，物块仍在长木板上，物块相对木板的位移为d，木板相对地面的位移为s。则在此过程中

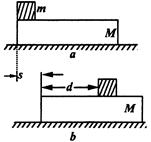
A．摩擦力对木板做功为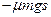
B．摩擦力对物块做功为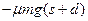
C．木板动能的增量为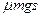
D．系统由于摩擦而产生的热量为

参考答案：BCD

本题解析：略

本题难度：简单

3、简答题  如图所示的电路中，两平行金属板A、B水平放置，两板间的距离d=40cm．电源电动势E=24V，内电阻r=1Ω，电阻R=15Ω．闭合开关S，待电路稳定后，将一带正电的小球从B板小孔以初速度v0=4m/s竖直向上射入板间．若小球带电量为q=1×10-2?C，质量为m=2×10-2?kg，不考虑空气阻力．那么，滑动变阻器接入电路的阻值为多大时，小球恰能到达A板？此时，电源的输出功率是多大？（取g=10m/s2）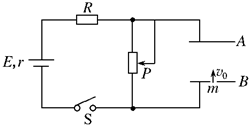

参考答案：（1）小球进入板间后，受重力和电场力作用，且到A板时速度为零．
设两板间电压为UAB
由动能定理得
-mgd-qUAB=0-12mv2?①
∴滑动变阻器两端电压?
U滑=UAB=8?V?②
设通过滑动变阻器电流为I，由欧姆定律得
I=E-U滑R+r=1A?③
滑动变阻器接入电路的电阻?
R滑=U滑I=8Ω?④
即滑动变阻器接入电路的阻值为8Ω时，小球恰能到达A板．
（2）电源的输出功率?
P出=I2（R+R滑）=23?W?⑤
故电源的输出功率是23W．

本题解析：

本题难度：一般

4、简答题  如图，两条水平虚线之间有垂直于纸面向里，宽度为d=50cm，磁感应强度为B=1.0T的匀强磁场．边长为l=10cm的正方形线圈，质量为m=100g，电阻为R=0.020Ω．线圈下边缘到磁场上边界的距离为h=80cm．将线圈由静止释放，已知其下边缘刚进入磁场和刚穿出磁场时刻的速度相同．取g=10m/s2．求：
（1）线圈进入磁场的过程中产生的电热Q．
（2）线圈下边缘穿越磁场的过程中，线圈的最小速度v．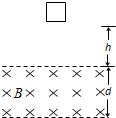

参考答案：（1）在线圈下边缘刚进入磁场到刚穿出磁场过程中用能量守恒定律，动能不变，重力势能的减小全部转化为电能，又转化为电热，
因此：Q=mgd=0.50J
（2）设线圈自由下落阶段的末速度v，即线圈下边缘到达磁场上边界时的瞬时速度大小是v0，
则v02=2gh，v0=4.0m/s?
线圈上边缘到达磁场上边界时线圈速度一定最小，在线圈进入磁场过程中用动能定理：
mgL-W=12mv2-12mv02
而克服安培力做的功W就等于增加的电能也等于产生的电热Q
因此解得：v=2

本题解析：

本题难度：一般

5、计算题  如图所示，BC是半径为R的1/4圆弧形光滑且绝缘的轨道，位于竖直平面内，其下端与水平绝缘轨道平滑连接，整个轨道处在水平向左的匀强电场中，电场强度为E，今有一质量为m、带正电q的小滑块，（体积很小可视为质点），从C点由静止释放，滑到水平轨道上的A点时速度减为零。若已知滑块与水平轨道间的动摩擦因数为μ，求：
（1）滑块通过A点时的速度大小；
（2）水平轨道上A、B两点之间的距离。

参考答案：解：（1）小滑块从C到B的过程中，只有重力和电场力做功。设滑块通过B点时的速度为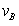，根据动能定理有：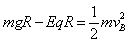
解得：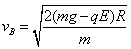
（2）设A、B两点间的距离为L，则滑块由C滑到A的过程中，由动能定理有：

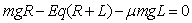
解得：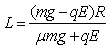

本题解析：

本题难度：一般