1、简答题  如图所示，在光滑水平长直轨道上有A、B两个绝缘体，它们之间有一根长为l的轻质软线相连接，其中A的质量为m，B的质量为M=4m，A为带有电荷量为q的正电荷，B不带电，空间存在着方向水平向右的匀强电场，场强大小为E。开始时用外力把A与B靠在一起并保持静止，某时刻撤去外力，A开始向右运动，直到细线绷紧。当细线被绷紧时，两物体将有极短时间的相互作用，而后B开始运动，且细线再次松弛。已知B开始运动时的速度等于线刚绷紧前瞬间A的速度的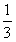。设整个过程中，A的电荷量都保持不变。
求细线第二次被绷紧的瞬间B对地的位移（相对于初始点）。

参考答案：

本题解析：由动能定理得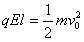
?（3分）
设细线第一次绷紧后的瞬间A的速度为v1,B的速度为v2，因细线绷紧过程所用时间极短，电场力的冲量极小，可以忽略不计，根据动量守恒定律有
?（3分）
第一次绷紧后A的速度为，负号表示速度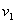的方向水平向左，
∴A又回到第一次绷紧的位置历时


∴不会相碰?（3分）
两者速度相同时，，?（2分）
此后再运动t′绷紧：??（3分）
?解得：??（3分）
∴?（3分）

本题难度：一般

2、简答题  如图所示，在光滑水平地面上有一质量为2m的长木板，其左端放有一质量为m的重物（可视为质点），重物与长木板之间的动摩擦因数为μ．开始时，长木板和重物都静止，现在给重物以初速度v0，设长木板撞到前方固定的障碍物前，长木板和重物的速度已经相等．已知长木板与障碍物发生弹性碰撞，为使重物始终不从长木板上掉下来，求长木板的长度L至少为多少？（重力加速度度为g）

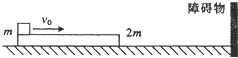
参考答案：碰撞前，长木板和重物的共同速度为v1，由动量守恒定律得：
mv0=3mv1；
碰撞后瞬间，长木板以速度v1反弹，最终两者的共同速度为v2．由动量守恒定律得：
2mv1-mv1=3mv2；
对全过程，由功能关系得：
μmgL=12mv20-12?3mv22
联立解得：L=13v2027μg
答：为使重物始终不从长木板上掉下来，长木板的长度至少为13v2027μg．

本题解析：

本题难度：一般

3、简答题  美国航空航天局和欧洲航空航天局合作研究的“卡西尼”号土星探测器，在美国东部时间2004年6月30日（北京时间7月1日）抵达预定轨道，开始“拜访”土星及其卫星家族．“卡西尼”号探测器进入绕土星飞行的轨道，先在半径为R的圆形轨道Ⅰ上绕土星飞行，运行速度大小为v1．为了进一步探测土星表面的情况，当探测器运行到A点时发动机向前喷出质量为△m的气体，探测器速度大小减为v2，进入一个椭圆轨道Ⅱ，运动到B点时再一次改变速度，然后进入离土星更近的半径为r的圆轨道Ⅲ，如图所示．设探测器仅受到土星的万有引力，不考虑土星的卫星对探测器的影响，探测器在A点喷出的气体速度大小为u．求：

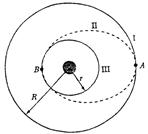
（1）探测器在轨道Ⅲ上的运行速率v3和加速度的大小；
（2）探测器在A点喷出的气体质量△m．

参考答案：（1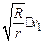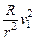），；（2）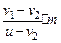

本题解析：（1）在轨道I上，探测器m所受万有引力提供向心力，设土星质量为M，则有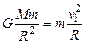
同理，在轨道Ⅲ上有
由上两式可得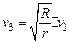
探测器在轨道Ⅲ上运行时加速度设为a，则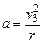
解得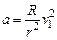
（2）探测器在A点喷出气体前后，由动量守恒定律，得mv1=(m－△m)v2＋△mv
解得

本题难度：一般

4、计算题  甲、乙两小船质量均为M＝120 kg，静止于水面上，甲船上的人质量m＝60 kg，通过一根长为L＝10 m的绳用F＝120 N的水平力拉乙船，求：
(1)两船相遇时，两船分别走了多少距离．
(2)为防止两船相撞，人至少以多大的速度跳离甲船．(忽略水的阻力)

参考答案：：(1)4 m　6 m　(2)4m/s

本题解析：：(1)甲船和人与乙船组成的系统动量时刻守恒．
由平均动量守恒得：(M＋m)x甲＝Mx乙
又x甲＋x乙＝L
以上两式联立可求得：x甲＝4 m，x乙＝6 m.
(2)设两船相遇时甲船的速度为v1，对甲船和人用动能定理得：
Fx甲＝(M＋m)v
因系统总动量为零，所以人跳离甲后，甲速度为零时，人跳离速度最小，设人跳离的速度为v，因跳离时，甲船和人组成的系统动量守恒，有：(M＋m)v1＝0＋mv可求得：v＝4m/s.

本题难度：一般

5、选择题  [物理选修3-5]（本题共2小题，每小题6分，共12分。每小题只有一个选项符合题意）
（1）测年法是利用衰变规律对古生物进行年代测定的方法。若以横坐标t表示时间，纵坐标m表示任意时刻的质量，为t＝0时的质量。下面四幅图中能正确反映衰变规律的是?。（填选项前的字母）

（2）如图所示，一个木箱原来静止在光滑水平面上，木箱内粗糙的底板上放着一个小木块。木箱和小木块都具有一定的质量。现使木箱获得一个向右的初速度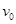，则?。（填选项前的字母）

A．小木块和木箱最终都将静止
B．小木块最终将相对木箱静止，二者一起向右运动
C．小木块在木箱内壁将始终来回往复碰撞，而木箱一直向右运动
D．如果小木块与木箱的左壁碰撞后相对木箱静止，则二者将一起向左运动

参考答案：（1）C?（2）B

本题解析：（1）设衰变周期为T，那么任意时刻14C的质量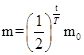，可见，随着t的增长物体的质量越来越小，且变化越来越慢，很显然C项图线符合衰变规律．
故选C．
（2）系统所受外力的合力为零，动量守恒，初状态木箱有向右的动量，小木块动量为零，故系统总动量向右，系统内部存在摩擦力，阻碍两物体间的相对滑动，最终相对静止，由于系统的总动量守恒，不管中间过程如何相互作用，根据动量守恒定律，最终两物体以相同的速度一起向右运动．
故选B．

本题难度：一般