1、计算题  （18分）如图所示，固定在水平地面上的工件，由AB和BD两部分组成，其中AB部分为光滑的圆弧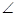，AOB=37o，圆弧的半径R=0．5m；BD部分水平，长度为0．2m，C为BD的中点。现有一质量m=lkg，可视为质点的物块从A端由静止释放，恰好能运动到D点。（g=10m/s2，sin37o=0．6，cos37o=0．8）求：

（1）物块运动到B点时，对工件的压力大小；
（2）为使物块恰好运动到C点静止，可以在物块运动到B点后，对它施加一竖直向下的恒力F，F应为多大?
（3）为使物块运动到C点时速度为零，也可先将BD部分以B为轴向上转动一锐角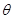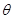，应为多大?（假设物块经过B点时没有能量损失）

参考答案：（1） 14N；（2） 10N；（3） 37°。

本题解析：（1）物块在AB部分下滑的过程中，由动能定理mgR（1－cos37°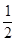）=mv2，
在B点，由牛顿第二定律FN－mg=，解得FN=14N。
由牛顿第三定律F压=FN=14N。
（2）物块在从A运动到D的过程中，由动能定理得
mgR（1－cos37°）－μ（mg+F）LBC=0
所以LBD=2LBC，解得F=10N。
（3）物块在从A经B运动到C的过程中，由动能定理
mgR（1－cos37°）－mgLBCsinθ－μmgLBCcosθ=0
代入数据得：1=sinθ+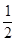cosθ，解得θ=37°。

本题难度：一般

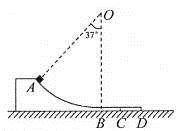
2、计算题  如图所示，与水平面成θ＝37°的粗糙斜面与一光滑圆轨道相切于A点，斜面AB的长度s＝2.3 m，动摩擦因数μ=0.5，圆轨道半径为R=0.6m。让质量为m=1kg物体(可视为质点)从B点以某一沿斜面向下的初速度释放，恰能沿轨道运动到圆轨道的最高点C，空气阻力忽略不计。(取sin37°＝0.6，cos37°＝0.8)

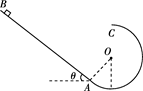
(1)求释放时的初动能；
(2)设物体从C点落回斜面AB上的P点，试通过计算判断P位置比圆心O高还是低．

参考答案：(1)9.2J(2)P位置比O点低

本题解析：（1）物体恰好能过轨道的最高点，则在C点的速度为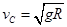,（1）
A点距离圆环轨道最低端的高度为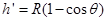（2）
根据动能定理可得：（3）
联立可得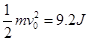
（2）如果恰好和圆心向平，则水平位移为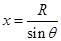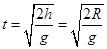，，算出

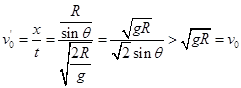
所以P位置比O点低
点评：本题是动能定理与牛顿定律的综合应用，关键在于研究过程的选择，中等难度．

本题难度：一般

3、选择题  如图所示，在平直轨道做匀变速运动的车厢中，用轻细线悬挂一个小球，悬线与竖直方向保持恒定的夹角θ，则?
?
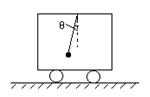A．小车一定具有方向向左的加速度
B．小车一定做匀速直线运动
C．小车的加速度大小为gtanθ
D．小车的加速度大小为gcotθ

参考答案：C

本题解析：小球所受合力，水平向右。A错。小车做匀变速直线运动，B错。小车与小球具有相同加速度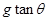，C对D错。

本题难度：简单

4、简答题  杂技演员在进行“顶杆”表演时，顶杆演员A顶住一根质量可忽略不计的长竹竿．质量为m=30kg的演员B自竹竿顶部由静止开始下滑，滑到竹竿底端时速度恰好为零．为了研究下滑演员B沿杆的下滑情况，在顶杆演员A与竹竿底部之间安装了一个力传感器．由于竹竿处于静止状态，传感器显示的就是下滑演员B所受摩擦力的情况，如图所示．g=10m/s2．求：
（1）下滑演员B下滑过程中的最大速度；
（2）竹杆的长度．

参考答案：（1）以人为研究对象，人加速下滑过程中受重力mg和杆对人的作用力F1，由题图可知，人加速下滑过程中杆对人的作用力F1为180 N．
由牛顿第二定律得
mg-F1=ma，
则a=4 m/s2．
1s末人的速度达到最大，则v=at1=4 m/s．
（2）加速下降时位移为：s1=12at12=2 m．
减速下降时，由动能定理得（mg-F2）s2=0-12mv2，
代入数据解得s2=4m，
杆的长度s=s1+s2=6m．
答：（1）杆上的人下滑过程中的最大速度为4m/s；
（2）竹竿的长度为6m．

本题解析：

本题难度：一般

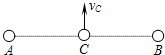
5、选择题  如图所示，A、B为两个固定的等量的正电荷，在它们连线的中点处有一个可以自由运动的正电荷C，现给电荷C一个垂直于连线的初速度v0，若不计电荷C所受的重力，则关于电荷C运动过程中的速度和加速度情况，下列说法正确的是（　　）
A．加速度始终增大
B．加速度先增大后减小
C．速度始终增大
D．速度先增大后减小