1、简答题  用长为L的绝缘细线拴一个质量为m，电荷量为q的小球，如图所示，线的另一端固定在水平方向的匀强电场中，开始时将带电球拉到使线成水平的位置，小球由静止从A点向下摆动，当细线转过60°角，小球到达B点时，速度恰好为零，试求：
（1）匀强电场的场强E为多大？
（2）小球由A运动到B点的过程中，细线的最大拉力多大？
（3）在A点给小球一竖直向下的初速度使小球能完成竖直平面内的完整的圆周运动，求小球速度最小的点的电势．（设O点的电势为零，电场区域足够大，小球始终在匀强电场中）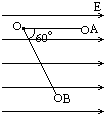

参考答案：（1）小球从A到B的运动过程中运用动能定理的：
-EqL（1-cos60°）+mgLsin60°=0
解得：E=

本题解析：

本题难度：一般

2、选择题  在距离地面15m高处，某人将一质量为4kg的物体以5m/s的速度水平抛出，则人对物体做的功为（　　）
A．20J
B．50J
C．600J
D．650J

参考答案：对人抛物体的过程，根据动能定理得：
W=12mv20=12×4×52J=50J，即人对物体做的功是50J．
故选：B．

本题解析：

本题难度：一般

3、简答题  如图1所示，轻弹簧一端固定在与斜面垂直的挡板上，另一端点在O位置．质量为m的物块A（可视为质点）以初速度v0从距O点为x0的P点沿斜面向下运动，与弹簧接触后压缩弹簧，将弹簧右端压到O′点位置后，A又被弹簧弹回．A离开弹簧后，恰好回到P点．物块A与斜面间的动摩擦因数为μ，斜面倾角为37°．求：
（1）O点和O′点间的距离x1．
（2）如图2若将另一个与A完全相同的物块B（可视为质点）与弹簧右端拴接，将A与B并排在一起，使弹簧仍压缩到O′点位置，然后从静止释放，A、B共同滑行一段距离后分离．分离后物块A沿斜面向上滑行的最大距离x2是多少？

参考答案：（1）A从向下运动到再次返回到P的过程，根据动能定理有：
2μmg(x0+x1)=12mv02
解得：x1=5v0216μg-x0
（2）A从O′到P过程设弹簧弹力做功为W，根据动能定理有：
W-μmg（x0+x1）cosθ-mgsinθ（x0+x1）=0
A、B将在弹簧原长处分离，设此时共同速度为v，根据动能定理有：W-2μmgx1cosθ-2mgx1sinθ=122mv12
分离后对A有：μmgx2cosθ+mgx2sinθ=12mv12
联立以上各式可得：x2=x0-5v0232μg．
答：（1）O点和O′点间的距离x1=5v0216μg-x0．
（2）分离后物块A沿斜面向上滑行的最大距离x2是x2=x0-5v0232μg．

本题解析：

本题难度：一般

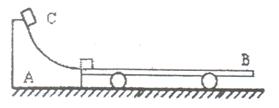
4、计算题  （20分）如图所示，A为一具有光滑曲面的固定轨道，轨道底端是水平的，质量M=30kg的小车B静止于轨道右侧，其板面与轨道底端靠近且在同一水平面上，一个质量m=10kg的物体C以初速度零从轨道顶滑下，冲上小车B后经一段时间与小车相对静止并继续一起运动。若轨道顶端与底端水平面的高度差h为0．80m，物体与小车板面间的动摩擦因数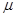为0．40，小车与水平面间的摩擦忽略不计，（取g=10m/s2），求：
（1）物体与小车保持相对静止时的速度；
（2）从物体冲上小车到与小车相对静止时小车位移；
（3）物体冲上小车后相对于小车板面滑动的距离。

参考答案：（1）1m/s?（2）3.75m?（3）1.5m

本题解析：（1）下滑过程机械能守恒
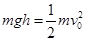，解得v0=4m/s?（3分）
物体相对于小车板面滑动过程动量守恒
mv0=（m+M）v ?
所以v=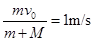?（3分）
（2）对小车由动能定理有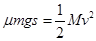?（4分）
可得s=3.75m?（2分）
（3）设物体相对于小车板面滑动的距离为L，由能量守恒有，摩擦生热：
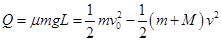?（6分）
代入数据解得：L=1.5m?（2分）

本题难度：一般

5、选择题  光滑的水平面上静置一个质量为M的木块，一质量为m的子弹以水平速度v1射入木块，以v2穿出，木块此后的速度为v．对这一过程正确的说法是（　　）
A．子弹对木块做的功等于木块获得的动能
B．子弹对木块做的功等于子弹克服摩擦力做的功
C．子弹损失的动能等于木块获得的动能加上子弹增加的内能
D．子弹和木块组成的系统机械能守恒

参考答案：A、以木块为研究对象，子弹对木块做的功等于木块获得的动能．故A正确．
? B、由于子弹与木块有相对位移，子弹对地位移大于木块对地位移，而两者相互作用力大小相等，则子弹对木块做的功大于子弹克服摩擦力做的功．故B错误．
? C、根据能量转化和守恒定律可知：子弹损失的动能转化为等于木块获得的动能加上系统增加的内能．故C错误．
? D、子弹和木块组成的系统机械能减小，转化为系统的内能．故D错误．
故选A

本题解析：

本题难度：简单