1、简答题  如图所示，竖直平面xOy内存在水平向右的匀强电场，场强大小E=10N/c，在y≥0的区域内还存在垂直于坐标平面向里的匀强磁场，磁感应强度大小B=0.5T一带电量q=+0.2C、质量m=0.4kg的小球由长l=0.4m的细线悬挂于P点小球可视为质点，现将小球拉至水平位置A无初速释放，小球运动到悬点P正下方的坐标原点O时，悬线突然断裂，此后小球又恰好能通过O点正下方的N点．（g=10m/s2），求：
（1）小球运动到O点时的速度大小；
（2）悬线断裂前瞬间拉力的大小；
（3）ON间的距离．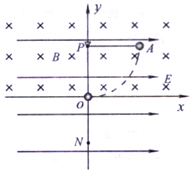

参考答案：（1）小球从A运到O的过程中，根据动能定理：12mvo2=mgl-qEl? ①
带入数据求得小球在O点速度为：vo=2m/s? ②
（2）小球运到O点绳子断裂前瞬间，对小球应用牛顿第二定律：T-mg-f洛=mvo2l? ③
? f洛=Bvoq? ④
②③④联立得：T=8.2N? ⑤
（3）绳断后，小球水平方向加速度? ax=F电m=Eqm=5m/s2? ⑥
小球从O点运动至N点所用时间? t=vNax=0.8s? ⑦
ON间距离? h=12gt2=3.2m? ⑧
答：小球运动到O点时的速度大小为2m/s，悬线断裂前瞬间拉力的大小为8.2N，ON间的距离为3.2m．

本题解析：

本题难度：一般

2、简答题  如图所示，有一电子（电量为e）经电压U0加速后，进入两块间距为d、电压为U的平行金属板间，
若电子从两板正中间垂直电场方向射入，且正好能穿过电场，求：
（1）电子进入偏转电场时的速度；（2）金属板AB的长度．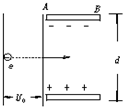

参考答案：（1）设电子被加速后速度大小为v0，对于电子在加速电场中由动能定理得：
eUo=12mv20? ①
?所以v0=

本题解析：

本题难度：一般

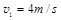3、选择题  质量为的小球以的速度与质量为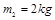的静止小球正碰，关于碰后速度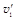与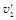，下面可能的是
A．==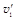
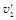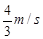
B．=，=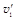
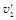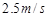
C．=，=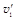
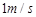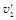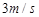
D．=，=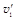

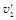参考答案：AB

本题解析：碰撞前总动量为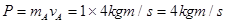．碰撞前总动能为
碰撞后总动量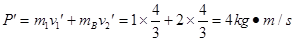，．碰撞后总动能为,符合能量守恒定律．故A正确．
碰撞后总动量．碰撞后总动能为,符合能量守恒定律，故B正确，
碰撞后总动量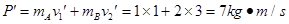，不符合动量守恒定律．故C错误．
碰撞后总动量．碰撞后总动能为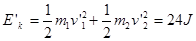，违反了能量守恒定律，D错误，
点评：对于碰撞过程，往往根据三个规律动量守恒、总动能不增加和符合物体的实际情况判断．

本题难度：一般

4、计算题  （16分）如图所示，水平光滑地面上停放着一辆小车，左侧靠在竖直墙壁上，小车的四分之一圆弧轨道AB是光滑的，在最低点B与水平轨道BC相切，BC的长度是圆弧半径的10倍，整个轨道处于同一竖直平面内。可视为质点的物块从A点正上方某处无初速下落，恰好落人小车圆弧轨道滑动，然后沿水平轨道滑行至轨道末端C处恰好没有滑出。已知物块到达圆弧轨道最低点B时对轨道的压力是物块重力的9倍，小车的质量是物块的3倍，不考虑空气阻力和物块落人圆弧轨道时的能量损失。求

（1）物块开始下落的位置距水平轨道BC的竖直高度是圆弧半径的几倍；
（2）物块与水平轨道BC间的动摩擦因数μ。

参考答案：（1）物块开始下落的位置距水平轨道BC的竖直高度是圆弧半径的4倍。
（2）μ= 0.3

本题解析：
（1）设物块的质量为m ，其开始下落处酌位置距BC的竖直高度为h，到达8点时的速度为v，小车圆弧轨道半径为R 。由机械能守恒定律，有
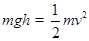?①
根据牛顿第二定律，有
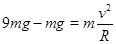?②
解得H = 4R?③
即物块开始下落的位置距水平轨道BC的竖直高度是圆弧半径的4倍。
（2）设物块与BC间的滑动摩擦力的大小为F，物块滑到C点时与小车的共同速度为v，物块在小车上由B运动到C的过程中小车对地面的位移大小为s 。依题意，小车的质量为3 m ，BC长度为10 R 。由滑动摩擦定律，有
F = μmg?④
由动量守恒定律，有
mv = （m + 3 m），?⑤
对物块、小车分别应用动能定理，有
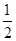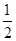F（10 R + s）="=" mv′2－mv2?⑥
Fs ="=" 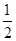（3 m）v′2－ 0?⑦
解得
μ= 0.3?⑧
评分标准：，
（1）8分，①、②式各3分，③式2分；
（2）8分，⑤、⑥、⑧式各2分，④、⑦式各1分。

本题难度：一般

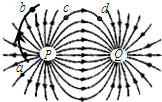
5、选择题  P、Q两电荷的电场线分布如图所示，c、d为电场中的两点．一个离子从a运动到b（不计重力），轨迹如图所示．则下列判断正确的是（　　）
A．P带负电
B．c、d两点电势相等
C．离子在运动过程中受到P的吸引
D．离子从a到b，电场力做正功