1、简答题  甲同学说：一个初速度为零、做匀加速直线运动的物体，第4 s内的平均速度肯定大于4 s内的平均速度。乙同学说：一个初速度为零，做匀加速直线运动的物体，第3秒末的速度等于第4 s初的速度。他们的说法对吗？说明理由。

参考答案：甲、乙都对。第4 s内的平均速度等于第3.5秒末的瞬时速度；4 s内的平均速度等于第2秒末的瞬时速度，故甲的说法正确。第3秒末与第4 s初是同一时刻，故乙的说法正确。

本题解析：

本题难度：一般

2、简答题  如图所示，一名消防队员在模拟演习训练中，沿着竖立在地面上的钢管往下滑．已知这名消防队员的质量为60kg他从钢管顶端由静止开始先匀加速再匀减速下滑到达地面时速度恰好为零．如果他加速时的加速度大小是减速时加速度的2倍，下滑的总时间为3s，下滑的总距离为12m，g取l0m/s2，求：
（1）该消防队员下滑过程中的最大速度；
（2）该消防队员加速下滑和减速下滑过程中分别受到的摩擦力大小．

参考答案：（1）设最大速度为v，加速的平均速度和减速的平均速度都是12v，故全程的平均速度为12v，故
h=.vt=12vt
解得
v=2ht=2×123m/s=8m/s
（2）加速过程
mg-f1=ma1
减速过程
f1-mg=ma2
根据速度时间公式，有
a1t1=a2t2=v
t1+t2=3
a1=2a2
12a1t21+12a2t22=h
解得
a1=8m/s2，a2=4m/s2；
f1=120N，f2=840N；
答：（1）该消防队员下滑过程中的最大速度为8m/s；
（2）该消防队员加速下滑过程中受到的摩擦力大小为120N，减速下滑过程中受到的摩擦力大小为840N．

本题解析：

本题难度：一般

3、计算题  磕头虫是一种不用足跳但又善于跳高的小甲虫。当它腹朝天、背朝地躺在地面上时，将头用力向后仰，拱起体背，在身下形成一个三角形空区，然后猛然收缩体内背纵肌，使重心迅速向下加速，背部猛烈撞击地面，地面反作用力便将其弹向空中。弹射录像显示，磕头虫拱背后重心向下加速（视为匀加速）的距离大约为h1=0.8 mm，弹射最大高度为h2=24 cm。而人原地起跳方式是先屈腿下蹲，然后突然蹬地向上加速，假想人的加速度与磕头虫加速过程的加速度大小相等，如果加速过程（视为匀加速）重心上升高度为H1=0.4 m，求人离地后重心上升的最大高度H2。（空气阻力不计，设磕头虫撞击地面和弹起的速率相等）

参考答案：解：设磕头虫加速下降的加速度大小为a，弹起时的速率为v1，则有
v12=2ah1
v12=2gh2
设人离地时的速率为v2，则有
v22=2aH1
v22=2gH2
解得：H2=120 m

本题解析：

本题难度：一般

4、计算题  一个热爱滑雪运动的人乘着雪橇从倾角为370的山坡匀变速滑下，他连同雪橇的总质量为80kg，从山坡滑下的初速度是1m/s，末速度是19 m/s，该山坡的长度为45m。求这位滑雪爱好者滑下山坡所用的时间及他下滑时所受到的平均阻力大小。（取重力加速度g=10m/s2, sin370=0.6，cos370=0.8）

参考答案：160N

本题解析：解由v2-v20=2as?3分
得a=4m/s2?2分
t=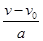=4.5s?2分
由牛顿第二定律mgsin370-f=ma?2分
f= mgsin370- ma=160N?3分
点评：本题难度较小，题干中给出了物体的运动过程，应根据运动学公式求解加速度，再由牛顿第二定律列公式求解

本题难度：简单

5、简答题  车从静止开始以1m/s2的加速度前进，车后与车相距s0为25m处有一人，与车开行方向相同，同时开始以6m/s的速度匀速追车，能否追上？若追不上，求人、车间的最小距离．

参考答案：设经过时间t他们速度相等，则
t=v人-v0a=6s
此时x人=v人t=36m
x车=12at2=18m
x人-x车=18m＜25m，所以不能追上
当速度相等时人和车的距离最小，
xmin=25m-18m=7m
答：不能追上，人、车间的最小距离为7m．

本题解析：

本题难度：一般