1、选择题 如图,竖直放置的斜面下端与光滑的圆弧轨道BCD的B端相切,圆弧半径为R,∠COB=q,斜面倾角也为q,现有一质量为m的小物体从斜面上的A点无初速滑下,且恰能通过光滑圆形轨道的最高点D.已知小物体与斜面间的动摩擦因数为m,求:
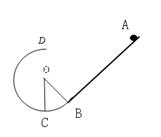
(1)AB长度l应该多大。
(2)小物体第一次通过C点时对轨道的压力多大。
参考答案:(1) 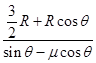 ?(2)
?(2)
本题解析:
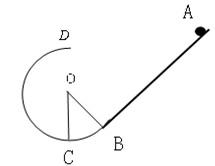
(1)因恰能过最高点D:
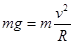 ? ( 1)? 2分
? ( 1)? 2分
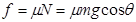 ?(2)? 1分
?(2)? 1分
物体从A运动到D全程,由动能定理:
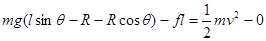 (3) 2分?
(3) 2分?
联立求得: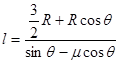 ? 2分
? 2分
(2)物体从C运动到D的过程,设C点速度为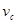 ,由机械能守恒定律:
,由机械能守恒定律:
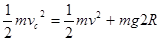 ? (4 )? 2分
? (4 )? 2分
物体在C点时:
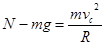 ?(5)? 2分
?(5)? 2分
联立求得: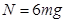 ?由牛顿第三定律可知,物体对轨道的压力是
?由牛顿第三定律可知,物体对轨道的压力是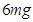 .? 1分
.? 1分
点评:中等难度。解决此类问题的常规思路是利用机械能守恒求速度和竖直平面内合外力等于向心力求外力,但如果机械能不守恒,一般用动能定理求解。
本题难度:一般
2、选择题 跳水运动员(视为质点)从10m跳台跳下,不计空气阻力,在运动员下落过程中,下列说法正确的是( )
A.运动员的机械能减少
B.运动员的动能减少
C.运动员的重力势能减少
D.以上说法都不对
参考答案:
A、因为不计空气阻力,运动员下落过程中只有重力做功,满足机械能守恒条件,故A错误;
B、因为运动员下落过程中,重力对运动员做正功,所以运动员的动能增加,故B错误;
C、据EP=mgh,运动员下落时,高度下降,故重力势能减少,故C正确;
D、因为C正确,故D错误.
故选C.
本题解析:
本题难度:简单
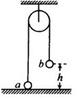
3、选择题 如图所示,一根很长、且不可伸长的柔软轻绳跨过光滑定滑轮,绳两端各系一个小球a和b。a球质量为m,静置于地面;b球质量为4m , 用手托住,高度为h,此时轻绳刚好拉紧。从静止开始释放b后,a能够达到的最大高度为(? )
A.3h
B.4h
C.1.6h
D.2.6h
参考答案:C
本题解析:把小球a,b看做一个整体,当小球b落地时,小球ab具有相同的速度v1,整个系统只有重力做功,机械能守恒,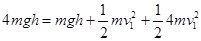 ,此后小球在重力作用下向上做匀减速直线运动,
,此后小球在重力作用下向上做匀减速直线运动,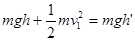 ,
,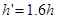 ,C选项正确。
,C选项正确。
点评:本题考查了系统机械能守恒定律的综合应用,在判断机械能守恒之前应首先判断是否满足条件,对于系统,机械能守恒可以看看是否出现第三种能量,若有则机械能不守恒。
本题难度:一般
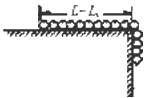
4、填空题 一根长为L的均匀绳索一部分放在光滑水平面上,长为L1的另一部分自然垂在桌面下,如图所示,开始时绳索静止,释放后绳索将沿桌面滑下,则绳索刚滑离桌面时的速度大小为____________。
参考答案: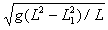
本题解析:
本题难度:一般
5、选择题 如图所示,ABC为竖直平面内的光滑绝缘轨道,其中AB为倾斜直轨道,BC为与AB相切的圆形轨道,并且圆形轨道处在匀强磁场中,磁场方向垂直纸面向里。质量相同的甲、乙、丙三个小球中,甲球带正电、乙球带负电、丙球不带电。现将三个小球在轨道AB上分别从不同高度处由静止释放,都恰好通过圆形轨道的最高点,则
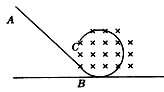
[? ]
A.经过最高点时,三个小球的速度相等
B.经过最高点时,甲球的速度最小
C.甲球的释放位置比乙球的高
D.运动过程中三个小球的机械能均保持不变
参考答案:CD
本题解析:
本题难度:一般