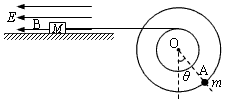
1、计算题  半径分别为r=0.1m和R=2r=0.2m的两个质量不计的圆盘，共轴固定连接在一起，可以绕水平轴O无摩擦转动，大圆盘的边缘上固定有一个可看作质点的质量m=0.1kg的小球A，小圆盘上绕有细线，细线的另一端与放在光滑绝缘水平桌面上的带电小物块B水平相连，物块B的质量M=0.12kg，带电量为q=1.0×10-4C，处于水平向左的匀强电场中，电场强度大小为E0=104N/C。整个系统在如图所示位置处于静止平衡状态，此时OA连线与竖直方向的夹角为θ。求：
（1）夹角θ的大小。
（2）缓慢顺时针转动圆盘，使小球A位于转轴O的正下方由静止释放，当圆盘转过45°角时物块B运动的速度多大？
（3）缓慢顺时针转动圆盘，使小球A重新回到转轴O的正下方，改变电场强度大小使其为E后由静止释放系统，物块B向左运动的最大距离s=，则电场强度E多大？

参考答案：解：（1）对物块B：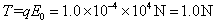
对圆盘，由力矩平衡：
得：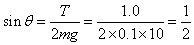
θ=30°
（2）对整个系统，由动能定理：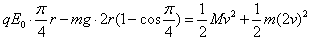
代入数据，解得：v=0.28m/s
（3），
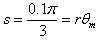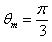
对整个系统，由动能定理：qE·=mg·2r(1－cos)
解得：E==9.55×103N/C

本题解析：

本题难度：困难

2、填空题  如图所示，质量为m、总长度为L的等边三角形ABC导线框，在A处用细线竖直悬挂于轻杆一端，水平轻杆另一端通过弹簧连接地面，离杆左端1/3处有一固定转轴O．现垂直于ABC施加一个水平方向广阔的匀强磁场，磁感强度为B，当在三角形ABC导线框中通以逆时针方向大小为I的电流时，AB边受到的安培力大小是______，此时弹簧对杆的拉力为______．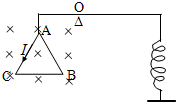

参考答案：因三角形的总长度为L，则AB的长度为L3，则AB边受到的安培力F=BIL3；
同理其他两边的安培力均为BIL3；BC边受到的安培力竖直向上，而BAC受到的等效安培力竖直向下，故三角形导线框受到的总安培力为0；
故左侧对轻杆的拉力为：
设轻杆长为S，则由力矩平衡可知：
mg13S=F23S
解得F=mg2；
故答案为：BIL3，mg2．

本题解析：

本题难度：一般

3、简答题  用如图所示装置做“研究有固定转动轴物体平衡条件”的实验，力矩盘上各同心圆的间距相等．
（1）在用细线悬挂钩码前，以下措施中必要的是______
A．判断力矩盘是否处在竖直平面；
B．判断横杆MN是否严格保持水平；
C．判断力矩盘与转轴间的摩擦是否足够小；
D．判断力矩盘的重心是否位于盘中心．
（2）在A、B二点分别用细线悬挂钩码，M、C两点用弹簧秤连接后，力矩盘平衡（如图所示），已知每个钩码所受的重力为0.49N，则由力矩平衡条件可推算出弹簧秤的示数为______N（已知弹簧秤的最小刻度是0.1N）．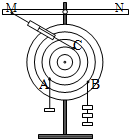

参考答案：（1）A、为了防止细线及弹簧称与力矩盘产生摩擦，判断力矩盘是否处在竖直平面是必要的．故A正确．
B、本实验与横杆MN是否平衡无关，没有必要检查横杆MN是否严格保持水平．故B错误．
C、D本实验要研究力矩盘平衡时砝码的拉力力矩和弹簧拉力力矩的关系，重力、摩擦力等影响要尽可能小，所以摩擦力要足够小，力矩盘的重心应在盘中心．故CD正确．
故选ACD．
（2）由图可知，A的力臂是2d，B的力臂是3d，F的力臂是2d，根据力矩的平衡得：F×2d+mg×2d=3mg×3d
解得：F=1.72N
故答案为：（1）ACD，（2）1.72

本题解析：

本题难度：一般

4、简答题  ?如图所示，质量为M=4kg的木板放置在光滑的水平面上，其左端放置着一质量为m=2kg的滑块(视作质点)，某时刻起同时给二者施以反向的力，如图，F1=6N，F2=3N，
适时撤去两力，使得最终滑块刚好可到达木板右端，且二者同时停止运动，已知力F2在t2=2s时撤去，板长为S=4.5m，g=10m/s2，求
小题1:? (1) ?力F1的作用时间t1
小题2:? (2)?二者之间的动磨擦因数μ
小题3:? (3)? t2=2s时滑块m的速度大小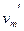

参考答案：
小题1:? (1)? t1=1s
小题2:? (2)?μ=0.1
小题3:? (3)?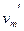=1m/s

本题解析：
小题1: (1)?以向右为正，?对整体的整个过程，由动量定理得?
F1t1-F2t2="0?" 代入数据得t1=1s
小题2:?在t1时间内，对m，由F合=ma得? F1-μmg=mam?代入数据可得am=2m/s2
m在t1时间内的位移大小S1=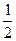am t12?代入数据得 S1=1m
同理在t2时间内，对M有? F2-μmg=MaM?代入数据得? aM=0.25m/s2
M在t2时间内的位移大小S2=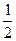aM t22?代入数据得 S2=1m
整个过程中，系统的机械能未增加，由功能关系得? F1S1+F2S2-μmgs="0?"
代入数据得μ=0.1
小题3:在t2=2s内，m先加速后减速，撤去F1后，m的加速度大小为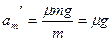=1m/s2?
所以m在t2=2s时的速度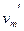=amt1-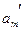(t2-t1)?代入数据得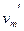=1m/s

本题难度：简单

5、计算题  如图所示，一个轻质直角形薄板ABC，AB=0.80m，AC="0.60" m，在A点固定一垂直于薄板平面的光滑转动轴，在薄板上D点固定一个质量为m=0.40kg的小球，现用测力计竖直向上拉住B点，使AB水平，如图（a），测得拉力F1=2.0N；再用测力计竖直向上拉住C点，使AC水平，如图（b），测得拉力F2=2.0N（g取10m/s2，sin37°=0.6，cos37°=0.8）。求：

（1）小球和转动轴的距离AD；
（2）在如图（a）情况下，将小球移动到BC边上距离A点最近处，然后撤去力F1，薄板转动过程中，AB边能转过的最大角度；
（3）在第（2）问条件下，薄板转动过程中，B点能达到的最大速度。

参考答案：(1)0.5m? (2)74°（3）2.32m/s

本题解析：（1）设小球D距AC为x，距AB为y。
根据力矩平衡得：
?
所以??
（2）设AD连线与AC边的夹角为θ，由几何关系可知。根据机械能守恒定律得AD边转过的最大角度是2θ，所以AB边转过的最大角度是2θ=74°
（3）根据机械能守恒定律，小球运动到最低点时，重力势能最小，动能最大

在转动过程中，薄板上各点角速度相同，所以

本题难度：一般