1、简答题  如图，质量均为m的两个小球A、B固定在弯成120°角的绝缘轻杆两端，OA和OB的长度均为l，可绕过O点且与纸面垂直的水平轴无摩擦转动，空气阻力不计．设A球带正电，B球带负电，电量均为q，处在竖直向下的匀强电场中．开始时，杆OB与竖直方向的夹角θ0=60°，由静止释放，摆动到θ=90°的位置时，系统处于平衡状态，求：
（1）匀强电场的场强大小E；
（2）系统由初位置运动到平衡位置，重力做的功Wg和静电力做的功We；
（3）B球在摆动到平衡位置时速度的大小v．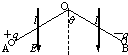

2、计算题  如图所示，竖直放置的两平行带电金属板间的匀强电场中有一根质量为m的均匀绝缘杆，上端可绕轴O在竖直平面内转动，下端固定一个不计重力的点电荷A，带电量＋q。当板间电压为U1时，杆静止在与竖直方向成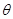＝45°的位置；若平行板以M、N为轴同时顺时针旋转＝15°的角，而仍要杆静止在原位置上，则板间电压应变为U2。求：U1/U2的比值。

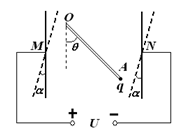
某同学是这样分析求解的：
两种情况中，都有力矩平衡的关系。设杆长为L，两板间距为d，当平行板旋转后，电场力就由变为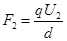，电场力对轴O的力臂也发生相应的改变，但电场力对轴O的力矩没有改变。只要列出两种情况下的力矩平衡方程，就可求解了。
你觉得他的分析是否正确？如果认为是正确的，请继续解答；如果认为有错误之处，请说明理由并进行解答。

3、简答题  半径分别为r=0.1m和R=2r=0.2m的两个质量不计的圆盘，共轴固定连接在一起，可以绕水平轴O无摩擦转动，大圆盘的边缘上固定有一个可看作质点的质量m=0.1kg的小球A，小圆盘上绕有细线，细线的另一端与放在光滑绝缘水平桌面上的带电小物块B水平相连，物块B的质量M=0.12kg，带电量为q=1.0×10-4C，处于水平向左的匀强电场中，电场强度大小为E0=104N/C．整个系统在如图所示位置处于静止平衡状态，此时OA连线与竖直方向的夹角为θ．求：
（1）夹角θ的大小．
（2）缓慢顺时针转动圆盘，使小球A位于转轴O的正下方由静止释放，当圆盘转过45°角时物块B运动的速度多大？
（3）缓慢顺时针转动圆盘，使小球A重新回到转轴O的正下方，改变电场强度大小使其为E后由静止释放系统，物块B向左运动的最大距离s=

4、填空题  如图为悬挂街灯的支架示意图，横梁BE质量为6kg，重心在其中点。直角杆A.DC重力不计，两端用铰链连接。已知BE=3m，BC=2m，∠A.CB=30°，横梁E处悬挂灯的质量为2kg，则直角杆对横梁的力矩为_______N·m，直角杆对横梁的作用力大小为_______N。（重力加速度g=l0m/s2）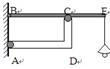

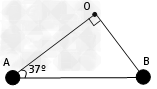
5、计算题  如图所示，OAB是一刚性轻质直角三角形支架，边长AB=0.2m，∠OAB=37°；在A、B两顶角处各固定一个大小不计的小球，质量均为1kg。支架可绕过O的水平轴在竖直平面内无摩擦地转动。（sin37°=0.6，cos37°=0.8，重力加速度g取10m/s2）
（1）为使支架静止时AB边水平，求在支架上施加的最小力；
（2）若将支架从AB位于水平位置开始由静止释放，求支架转动过程中A处小球速度的最大值。