1、简答题  如图，两个带同种电荷的小球A和B，A、B的质量分别为m和2m．开始时将它们固定在绝缘的光滑水平面上保持静止，A、B相距为d．A、B间的相互作用为遵守牛顿第三定律．现同时释放A、B，经过一段时间，A、B相距2d，此时B的速度大小为v．
求：（1）此时A的速度大小．
（2）此过程中B对A做的功．
（3）此过程中A球移动的距离．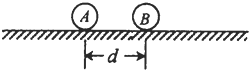

2、计算题  如图所示，以A、B和C、D为端点的两半圆形光滑轨道固定于竖直平面内，一滑板静止在光滑水平地面 上，左端紧靠B点，上表面所在平面与两半圆分别相切于B、C。一物块被轻放在水平匀速运动的传送带上E点，运动到A时刚好与传送带速度相同，然后经A沿半圆轨道滑下，再经B滑上滑板，滑板运动到C时被牢固粘连。物块可视为质点，质量为m，滑板质量M=2m，两半圆半径均为R，板长l=6.5R，板右端到C的距离L在R＜L＜5R范围内取值，E距A为s=5R，物块与传送带、物块与滑板间的动摩擦因数均为μ=0.5，重力加速度取g。
(1)求物块滑到B点的速度大小。
(2)试讨论物块从滑上滑板到离开滑板右端的过程中，克服摩擦力做的功Wf与L的关系，并判断物块能否滑到CD轨道的中点。

3、计算题  (10分）如图所示，半径为R的四分之一圆弧轨道放在水平面上，且圆弧上端切线竖直，下端与水平面平滑相切。另有一质量为m的小球以速度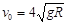冲上圆弧轨道，已知圆弧轨道的质量M=3m，不计摩擦和空气阻力，

求：(1)小球冲出圆弧轨道后能继续上升的最大高度h=?
(2)在小球上升h的过程中圆弧轨道移动的距离S=？

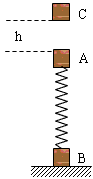
4、实验题  甲、乙两小孩各乘一辆小车在光滑水平面上匀速相向行驶，速度均为6 m/s，甲车上有质量m0＝1 kg的小球若干个，甲和他的车及所带小球总质量为m1＝50 kg，乙和他的车的总质量为m2＝30 kg，甲不断地将小球以16.5 m/s的对地水平速度抛向乙，并被乙接住，问甲至少要抛出________________个小球才能保证两小车不相撞(不计空气阻力)

5、计算题  如图所示，A、B两物体与一轻质弹簧相连，静止在地面上，有一小物体C从距A物体h高度处由静止释放，当下落至与A相碰后立即粘在一起向下运动，以后不再分开，当A与C运动到最高点时，物体B对地面刚好无压力、设A、B、C三物体的质量均为m，弹簧的劲度k，不计空气阻力且弹簧始终处于弹性限度内。若弹簧的弹性势能由弹簧劲度系数和形变量决定，求C物体下落时的高度h。