1、简答题  如图，两个带同种电荷的小球A和B，A、B的质量分别为m和2m．开始时将它们固定在绝缘的光滑水平面上保持静止，A、B相距为d．A、B间的相互作用为遵守牛顿第三定律．现同时释放A、B，经过一段时间，A、B相距2d，此时B的速度大小为v．
求：（1）此时A的速度大小．
（2）此过程中B对A做的功．
（3）此过程中A球移动的距离．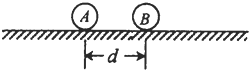

参考答案：（1）以A、B为研究对象，由动量守恒定律?mAvA=mBv?
求出vA=2v?
（2）对A，由动能定理，得到：
W=12mAv2A=2mv2
（3）由于两个球的合力相等，故加速度之比等于质量之比的倒数，为2：1；由于初速度为零，故任意时刻速度之比等于加速度之比，为2：1；故全程的平均速度之比为2：1；故位移之比为2：1，即：
sAsB=vAvB=21
其中：sA+sB=d?
联立求解得到：sA=2d3
答：（1）此时A的速度大小为2v．
（2）此过程中B对A做的功为2mv2．
（3）此过程中A球移动的距离为2d3．

本题解析：

本题难度：一般

2、计算题  如图所示，以A、B和C、D为端点的两半圆形光滑轨道固定于竖直平面内，一滑板静止在光滑水平地面 上，左端紧靠B点，上表面所在平面与两半圆分别相切于B、C。一物块被轻放在水平匀速运动的传送带上E点，运动到A时刚好与传送带速度相同，然后经A沿半圆轨道滑下，再经B滑上滑板，滑板运动到C时被牢固粘连。物块可视为质点，质量为m，滑板质量M=2m，两半圆半径均为R，板长l=6.5R，板右端到C的距离L在R＜L＜5R范围内取值，E距A为s=5R，物块与传送带、物块与滑板间的动摩擦因数均为μ=0.5，重力加速度取g。
(1)求物块滑到B点的速度大小。
(2)试讨论物块从滑上滑板到离开滑板右端的过程中，克服摩擦力做的功Wf与L的关系，并判断物块能否滑到CD轨道的中点。

参考答案：解：(1)物块先做匀加速直线运动，滑动摩擦力做正功，到A点时恰好与传送带的速度相等，然后沿光滑的半圆滑下来。设物块滑到B点时的速度为vB，对物块运动的整个过程由能量关系有：

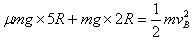
解得：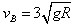
(2)假设物块和滑板能够达到共同的速度，设为v共，以物块和滑板组成的系统为研究对象，由动量守恒定律：mvB=(M+m)v共
设物块在滑板上的相对位移为△s，由能量守恒定律有：μmg△s=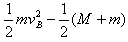v共2
由以上两式得：△s=6R<6.5R，所以滑块没有掉下来
设这个过程中滑板前进的位移为s，以滑板为研究对象，由动能定理得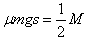：v共2
解得：s=2R
物块的对地位移：s1=2R+△s=8R
当2R≤L<5R时，滑块先做匀减速运动，再做匀速运动，滑板碰撞静止后，物块再做匀减速运动，滑上C点，再沿圆周运动
由动能定理：
解得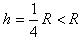：，所以滑块不能滑到CD轨道的中点

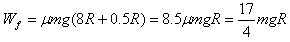
当R＜L＜2R时，滑块先做匀减速运动，在没有和滑板达到共同速度之前，滑板碰撞静止，滑块仍然向前滑动，到C点，然后滑上轨道。若恰好能上升到中点，则应满足-μmg(L+6.5R)-mgh=
解得：L=0.5R
L越小越容易上到中点，但R＜2L＜2R，故物块不能上升到CD轨道的中点
Wf=μng(L+6.5R)

本题解析：

本题难度：困难

3、计算题  (10分）如图所示，半径为R的四分之一圆弧轨道放在水平面上，且圆弧上端切线竖直，下端与水平面平滑相切。另有一质量为m的小球以速度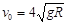冲上圆弧轨道，已知圆弧轨道的质量M=3m，不计摩擦和空气阻力，

求：(1)小球冲出圆弧轨道后能继续上升的最大高度h=?
(2)在小球上升h的过程中圆弧轨道移动的距离S=？

参考答案：(1) 5R(2)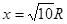

本题解析：由水平动量守恒得：，共同的水平速度为
由能量守恒得，解得：，所以又上升的高度为5R,
(2)水平移动的距离为：得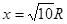
点评：在求解本题过程中明确小球运动到最高点时两者水平速度相等，小球竖直速度为零是本题的突破口，整个系统没有摩擦力和能量的损失，所以系统的机械能是守恒的，这是求解本题的关键

本题难度：一般

4、实验题  甲、乙两小孩各乘一辆小车在光滑水平面上匀速相向行驶，速度均为6 m/s，甲车上有质量m0＝1 kg的小球若干个，甲和他的车及所带小球总质量为m1＝50 kg，乙和他的车的总质量为m2＝30 kg，甲不断地将小球以16.5 m/s的对地水平速度抛向乙，并被乙接住，问甲至少要抛出________________个小球才能保证两小车不相撞(不计空气阻力)

参考答案：15

本题解析：当甲、乙两车最终速度相等时，两车刚好不相撞，设此速度为v，取甲运动方向为正方向，甲、乙两车及球组成的系统水平方向动量守恒，有：m1v1－m2v2＝(m1＋m2)v又v1＝v2＝6 m/s，将质量代入解得v＝1.5 m/s，方向与甲原运动方向相同，设抛出几个球后使甲的速度为v，对甲和被抛出的球，由动量守恒定律有m1v1＝nm0v0＋(m1－nm0)v，其中v0＝16.5 m/s,则n＝15个。

本题难度：简单

5、计算题  如图所示，A、B两物体与一轻质弹簧相连，静止在地面上，有一小物体C从距A物体h高度处由静止释放，当下落至与A相碰后立即粘在一起向下运动，以后不再分开，当A与C运动到最高点时，物体B对地面刚好无压力、设A、B、C三物体的质量均为m，弹簧的劲度k，不计空气阻力且弹簧始终处于弹性限度内。若弹簧的弹性势能由弹簧劲度系数和形变量决定，求C物体下落时的高度h。

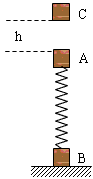
参考答案：解：开始时A处于平衡状态，有　　　　
当C下落h高度时速度为v，则有：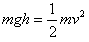　　　　
C与A碰撞粘在一起时速度为v"，由动量守恒有：　　　　
当A与C运动到最高点时，B对地面无压力，即：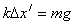　　　
可得：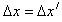　　
所以最高点时弹性势能与初始位置弹性势能相等
由机械能守恒有：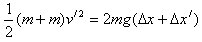　　　　
解得：

本题解析：

本题难度：困难