1、选择题  一辆汽车从静止开始由甲地出发，沿平直公路开往乙地。汽车先做匀加速运动历时t，接着做匀减速运动历时2t，开到乙地刚好停止。那么在匀加速运动、匀减速运动两段时间内
A．加速度大小之比为3：1
B．加速度大小之比为2：1
C．平均速度大小之比为1：2
D．平均速度大小之比为1：1

参考答案：：BD

本题解析：：根据速度公式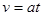，由于匀加速和匀减速时间之比1：2，故加速度大小之比为2：1，A错误、B正确；平均速度均为，C错误、D正确。

本题难度：简单

2、选择题  正在水平路面上行驶的汽车车厢底部有一质量为的木块，在车厢的顶部用细线悬挂一质量为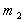的小球，某段时间内，乘客发现细线与竖直方向成θ角，而木块则始终相对于车厢静止，由此可以判断

[? ]
A．这段时间内，汽车可能正在向左匀加速行驶
B．这段时间内，汽车可能正在向右匀加速行驶
C．这段时间内，木块对车厢底部的摩擦力大小为gtanθ
D．这段时间内，木块对车厢底部的摩擦力为零

参考答案：AC

本题解析：

本题难度：一般

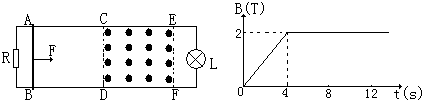
3、简答题  如图所示，水平面上有两电阻不计的金属导轨平行固定放置，间距d?为0.5米，左端通过导线与阻值为2欧姆的电阻R连接，右端通过导线与阻值为4欧姆的小灯泡L连接；在CDEF矩形区域内有竖直向上均匀磁场，CE长为2米，CDEF区域内磁场的磁感应强度B如图所示随时间t变化；在t=0s时，一阻值为2欧姆的金属棒在恒力F作用下由静止从AB位置沿导轨向右运动，金属棒与金属导轨的摩擦力为0.2N．当金属棒从AB位置运动到EF位置过程中，小灯泡始终正常发光．求：
（1）小灯泡的额定电流强度；
（2）恒力F的大小；
（3）运动到EF位置过程中金属棒的最大动能．

参考答案：（1）在金属棒棒未进磁场，电路中总电阻：R总=RL+R2=4+1=5Ω?
线框中感应电动势：E1=△φ△t=△BS△t=2×2×0.54V=0.5V
灯泡的额定电流强度：IL=ER总=0.55A=0.1A
（2）因灯泡中亮度不变，故在4秒末金属棒棒刚好进入磁场，且作匀速直线运动，
此时金属棒棒中的电流强度：I=IL+IR=IL+ILRLR=0.1+0.1×42A=0.3A
恒力F的大小：F=FA+f=BId+f=2×0.3×0.5?N+0.2N=0.5?N?
（3）金属棒产生感应电动势：E2=I(R+RLRRL+R)=0.3×(2+2×42+4)V=1V
金属棒在磁场中的速度：v=E2Bd=12×0.5m/s=1m/s
金属棒的加速度：a=vt=14m/s2
据牛顿第二定律，金属棒的质量：m=F-fa=0.30.25kg=1.2kg
Ek=mv22=0.6J?
答：（1）小灯泡的额定电流强度0.1A；
（2）恒力F的大小0.5N；
（3）运动到EF位置过程中金属棒的最大动能为0.6J．

本题解析：

本题难度：一般

4、选择题  下列情况可能出现的是
A．加速度增大，速度减小
B．速度为零，加速度不为零
C．加速度不为零，速度不变
D．加速度变化，速度不变

参考答案：AB

本题解析：当物体做减速运动时，加速度增大，速度在减小，所以A可能出现，当物体速度减小到零时，开始反向加速过程中会出现速度为零，但加速度不为零的情况，B正确，只要存在加速度，物体的速度总会发生改变，CD不可能出现，

本题难度：简单

5、计算题  如图10所示，斜面体固定在水平面上，斜面光滑，倾角为θ，斜面底端固定有与斜面垂直的挡板，木板下端离地面高H，上端放着一个小物块．木板和物块的质量均为m，相互间最大静摩擦力等于滑动摩擦力kmgsin θ(k>1)，断开轻绳，木板和物块沿斜面下滑．假设木板足够长，与挡板发生碰撞时，时间极短，无动能损失，空气阻力不计．求：

(1)木板第一次与挡板碰撞弹起上升过程中，物块的加速度；
(2)从断开轻绳到木板与挡板第二次碰撞的瞬间，木板运动的路程s；
(3)从断开轻绳到木板和物块都静止，摩擦力对木板及物块做的总功W.

参考答案：(1)(k－1)gsin θ　沿斜面向上　(2) 　(3)－

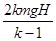
本题解析：(1)设木板第一次上升过程中，物块的加速度为a物块
由牛顿第二定律kmgsin θ－mgsin θ＝ma物块
解得a物块＝(k－1)gsin θ，方向沿斜面向上．
(2)设以地面为零势能面，木板第一次与挡板碰撞时的速度大小为v1
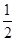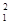由机械能守恒得：×2mv＝2mgH
解得v1＝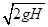
设木板弹起后的加速度为a板，由牛顿第二定律得：
a板＝－(k＋1)gsin θ
木板第一次弹起的最大路程s1＝＝
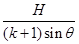
木板运动的路程s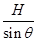＝＋2s1＝.
(3)设物块相对木板滑动距离为L
根据能量守恒mgH＋mg(H＋Lsin θ)＝kmgsin θL
摩擦力对木板及物块做的总功W＝－kmgsin θL
解得W＝－.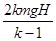

本题难度：一般