1、选择题  物体自楼顶处自由落下（不计空气阻力），落到地面的速度为v．在此过程中，物体从楼顶落到楼高一半处所经历的时间为
A.
B.
C.
D.

参考答案：C

本题解析：分析：设楼顶到地面的高度为h，物体从楼顶落到楼高一半处的速度为v′两次运用匀变速直线运动位移与速度的关系及速度时间关系即可求解．
解答：设楼顶到地面的高度为h，物体从楼顶落到楼高一半处的速度为v′则有：
? 2gh=v2?
? 2g=v′2
解得：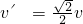
t=
故选C．
点评：本题考查的是自由落体运动基本公式的直接应用，难度不大，属于基础题．

本题难度：一般

2、选择题  做自由落体运动的物体，下列说法正确的是
A.第1s内、第2s内通过的位移相同
B.第1s内、第2s内速度的变化量相同
C.通过第一个1m、第二个1m所用时间相同

参考答案：B

本题解析：分析：自由落体运动是初速度为零的匀加速直线运动的一个特例，所以初速度为零的匀加速直线运动的规律对于自由落体运动也是适用的，此题可以应用这些规律来求解．
解答：
A、对于初速度为零的匀加速直线运动，第1s内、第2s内通过的位移之比为12：22，选项A错误．
B、速度的变化量△v=at，时间间隔相同，速度的变化量就相同．选项B正确．
C、对于初速度为零的匀加速直线运动，通过第一个1m、第二个1m所用时间比为1：（），选项C错误．
故答案为B．
点评：本题就是考察应用初速度为零的匀加速直线运动的特殊规律解答问题．特殊规律有：
①、1T末，2T末，3T末…瞬时速度的比为v1：v2：v3：…：vn=1：2：3：…：n
②、1T内，2T内，3T内…位移的比为S1：S2：S3：…：Sn=12：22：32：…：n2．
③、第一个T内，第二个T内，第三个T内…位移的比为SⅠ：SⅡ：SⅢ…SN=1：3：5：…：（2n-1）
④、从静止开始通过连续相等的位移所用的时间比为t1：t2：t3：…：tn=1：（）：（）：…：（）

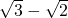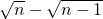本题难度：一般

3、选择题  为了求高层建筑的高度，从楼顶上自由下落一光滑小石子，除了知道当地的重力加速度以外，还需要知道下述哪个量①第一秒末的速度；②第一秒内的位移；③最后一秒的位移；?④最后一秒的初速度
A.①或②
B.①或③
C.③或④
D.②或④

参考答案：C

本题解析：分析：为了求高层建筑的高度，根据h=gt2，知道石子落地的时间，即可知道高度；根据v2=2gh，知道石子落地的速度，也可知道高度．
解答：①、知道第一秒末的速度，无法得到运动的总时间，也无法求出最后的速度，故无法求出高度，故①错误；
②、自由落体运动第一秒内的位移h=gt2=5m；无法得到运动的总时间，也无法求出最后的速度，故无法求出高度，故②错误；
③、知道最后一秒的位移，由于最后一秒的加速度、时间也是已知的，先根据位移时间关系公式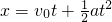求初速度，然后根据vt=v0+gt求出末速度，最后再根据v2=2gh求高度，故③正确；
④、知道最后一秒的初速度，由于最后一秒的加速度、时间也是已知的，故先根据vt=v0+gt求出末速度，然后再根据v2=2gh求高度，故④正确；
故选C．
点评：解决本题的关键要求出自由落体运动的时间或者末速度，可以根据h=gt2，也可以根据v2=2gh求高度．

本题难度：一般

4、选择题  一物体从H高处自由下落，经t时间落地．则当它下落t时间所下落的高度为
A.
B.
C.
D.

参考答案：C

本题解析：分析：物体做的是自由落体运动，根据自由落体的位移公式可以求得．
解答：物体做自由落体运动，
由H=gt2，
当时间为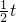时，物体下落的高度为 h==
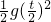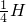
故选C．
点评：本题是对自由落体运动公式的直接应用，题目比较简单．

本题难度：困难

5、选择题  关于自由落体运动，下列说法正确的是
A.物体从静止开始下落的运动，叫做自由落体运动
B.如果空气阻力比重力小很多，空气阻力可以忽略不计，这时由静止开始下落的运动称为自由落体运动
C.跳伞运动员从飞机中由静止开始下落，打开伞以前的运动为自由落体运动，打开伞以后的运动不是自由落体运动
D.一雨滴从屋顶落下，途中经过一窗子时，经过窗子的这一段运动为自由落体运动

参考答案：C

本题解析：自由落体运动是初速度为零、只受重力作用的运动，必须同时具备这两个条件．A、B中没有叙述物体只受重力作用，所以错误．C中符合这两个条件，正确．D中经过窗子的一段运动的初速不为零，因而错误．

本题难度：困难