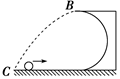
1、计算题  如图所示，一光滑的半径为R的半圆形轨道放在水平面上，一个质量为m的小球以某一速度冲上轨道，然后小球从轨道口B处飞出，最后落在水平面上，已知小球落地点C距B处的水平距离为3R.求小球对轨道口B处的压力为多大？

参考答案：5mg/4

本题解析：在平抛运动中2R=gt2/2?
3R=vBt
vB=3√gR/2
轨道对球压力FN+mg="m" vB2/R
FN="5mg/4"
球对轨道的压力FN′＝5mg/4
点评：本题难度较小，在最高点由支持力和重力的合力提供向心力，结合平抛运动规律求解

本题难度：一般

2、选择题  下列哪个运动是抛体运动
A．随电梯一起运动的物体的运动
B．抛向空中的细绳的运动
C．抛向空中的纸片的运动
D．抛向空中的铅球的运动

参考答案：D

本题解析：
试题分析: 随电梯一起运动的物体的运动不是抛体运动，因为电梯对物体有作用力．故A错误；抛向空中的细绳，是由于空气阻力的影响较大，不能看成抛体运动．故B错误；抛向空中的纸片的运动，不是抛体运动，由于空气阻力对纸片的运动影响较大，不能忽略．故C错误；抛向空中的铅球，空气阻力相比于重力可忽略不计，所以其运动可以看成抛体运动．故D正确。

本题难度：简单

3、选择题  将一个物体以速度v水平抛出，当物体的速度变到与水平速度的夹角为45°的过程中所经历的时间为（　　）
A．v/g
B．v/（2g）
C．2v/g
D．

参考答案：由题意可知，tan45°=vyv0=1
所以vy=v
竖直方向做自由落体运动，所以t=vyg=vg
故选A

本题解析：

本题难度：一般

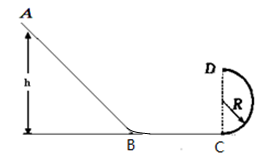
4、计算题  （12分）如图，固定在水平面上组合轨道，由光滑的斜面、光滑的竖直半圆(半径R=2.5m)与粗糙的水平轨道组成；水平轨道动摩擦因数μ=0.25，与半圆的最低点相切，轨道固定在水平面上。一个质量为m=0.1kg的小球从斜面上A处静止开始滑下，并恰好能到达半圆轨道最高点D，且水平抛出，落在水平轨道的最左端B点处。不计空气阻力，小球在经过斜面与水平轨道连接处时不计能量损失，g取10m/s2。求：

（1）小球出D点的速度v；
（2）水平轨道BC的长度x；
（3）小球开始下落的高度h。

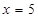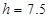参考答案：（1）5 m/s（2）m（3）m

本题解析：（1）小球恰好能到达半圆轨道最高点D，由牛顿第二定律得
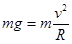                ①     （3分）
代入数据得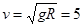 m/s        （1分）
(2)小球离开D点做平抛运动
水平方向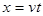     ②（2分）
竖直方向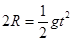     ③（2分）
由②③解得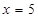m     （1分）
（3）从A至D过程，由动能定理得
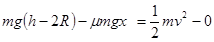 ④（2分）
代入数据得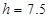m（1分）
考点：牛顿第二定律，动能定理

本题难度：一般

5、简答题  某人在距地面2m高处，将质量为2kg的小球以3m/s的速度水平抛出（取g=10m/s2）．求：
（1）人抛球时对球做多少功？
（2）若不计空气阻力，小球落地时速度的大小？
（3）若小球落地时速度大小是5m/s，则小球在空中克服阻力做多少功？

参考答案：（1）根据动能定理得，人抛球时对球做功W=12mv02=12×2×9J=9J．
（2）根据动能定理得，mgh=12mv2-12mv02
解得v=

本题解析：

本题难度：一般