1、简答题  质量为M的木块在水平面上处于静止状态，有一质量为m的子弹以水平速度v0击中木块并与其一起运动，若木块与水平面之间的动摩擦因数为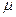，则木块在水平面上滑行的距离为多少？
某同学解题时立出了动量守恒方程：……①
还立出了能量守恒方程：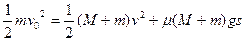
并据此得出结果。这种解法正确吗？
如果是正确的，请求出结果；如果是错误的，请说明所列出的有关方程成立的条件或错
的原因，并假设此条件成立，再纠正错误，求出结果。

参考答案：这种解法是错误的。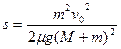

本题解析：这种解法是错误的。
方程①只适用于子弹与木块相互作用时间极短、地面滑动摩擦力冲量可以忽略不计的情况
方程②没有考虑子弹与木块碰撞时损失的机械能
第二个方程应写为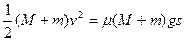
与方程①联立解得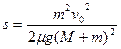

本题难度：简单

2、简答题  如图所示，长为L的木板A右边固定着一个挡板，包括挡板在内的总质量为1.5M，静止在光滑的水平地面上。有一质量为M的小木块B，从木板A的左端开始以初速度v0在
木板A上滑动。小木块B与木板A间摩擦因数为μ，小木块B滑到木板A的右端与挡板发生碰撞。已知碰撞过程时间极短，且碰后木块B恰好滑到木板A的左端就停止滑动。
（1）若μL=3v02/160g，在小木块B与挡板碰撞后的运动过程中，摩擦力对木板A做正功还是负功？做了多少？
（2）讨论木板A和小木块B在整个过程中，是否有可能在某一段时间内相对地面运动方向是向左的。如果不可能，说明理由；如果可能，求出至少可能向左滑动、又能保证木板A和小木块B刚好不脱离的条件。

参考答案：
（1）摩擦力对木板做负功，大小为（27/400）M v02
（2）B向左滑又不脱离A的条件是2v02/15g＜μL≤3v02/20g

本题解析：（1）设B与A碰撞后A、B的速度分别为vA、vB，最终A、B的共同速度为v，则由动量守恒、能量守恒有mBv0=mAvA+mBvB，mBv0=（mA+mB）v
μmBgL=（1/2）mAvA2+（1/2）mBvB2-（1/2）（mA+mB）v2
又μL=3v02/160g
以上各式联列解得v=（2/5）v0，vA=（1/2）v0，vB=（1/4）v0
或v=（2/5）v0，vA=（3/10）v0，vB=（11/20）v0
分析上述两组结果，由于两物碰撞后均与v0同向，而其中第二组结果vA=（3/10）v0＜vB=（11/20）v0，该速度关系与实际不符，舍去
因此，由动能定理可得摩擦力做功
Wf =（1/2）（1.5M）v2-（1/2）（1.5M）vA2=-（27/400）M v02
即摩擦力对木板做负功，大小为（27/400）M v02
（2）整个过程动量守恒，A不可能向左运动，碰后B可能。
要使B向左运动，由动量守恒、能量守恒有
mBv0=mAvA+mBvB，mBv0=（mA+mB）v
μmBgL=（1/2）mAvA2+（1/2）mBvB2-（1/2）（mA+mB）v2? vB＜0
以上各式联列解得μL＞2v02/15g
要保证A和B不脱离，由动量守恒和能量守恒有
mBv0=（mA+mB）v
2μmBgL≥（1/2）mBv02-（1/2）（mA+mB）v2
解得μL≤3v02/20g
故B向左滑又不脱离A的条件是2v02/15g＜μL≤3v02/20g

本题难度：一般

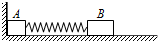
3、简答题  如图，质量分别为m和3m的物块A、B用一根轻弹簧相连，置于光滑的水平面上，物块A刚好与墙壁接触．先用外力缓慢向左推物块B使弹簧压缩，此过程中外力做的功为W，然后突然撤去外力．求：
①物块A刚离开墙壁时物块B的速度；
②在物块A离开墙壁后的运动过程中，物块A、B各自的最小速度．

参考答案：①设物块A刚离开墙壁时物块B的速度为v，撤去外力后，以弹簧和物块B组成的系统为研究对象，
由机械能守恒定律可得：W=12?3mv2，解得：v=

本题解析：

本题难度：简单

4、选择题  质量不等但有相同动能的两物体，在摩擦系数相同的水平地面上滑行直到停止，则
A.质量大的物体滑行距离大
B.质量小的物体滑行距离大
C.它们滑行的距离一样大
D.它们克服摩擦力所做的功一样多

参考答案：B

本题解析：

本题难度：困难

5、选择题  关于物体的动量，下列说法哪些是正确的(? )
A．物体的动量越大，其惯性越大
B．同一物体的动量越大，其速度一定越大
C．物体的动量越大，其受到的作用力一定越大
D．动量的方向一定是沿物体运动的方向

参考答案：BD

本题解析：惯性大小的唯一量度是物体的质量，如果物体的动量大，但也有可能物体的质量很小，所以不能说物体的动量大其惯性就大，故A错误；动量等于物体的质量与物体速度的乘积，即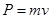，同一物体的动量越大，其速度一定越大，故B正确．力的大小决定物体的加速度的大小，与物体的速度无关，所以也与物体的动量的大小无关，故C错误．动量等于物体的质量与物体速度的乘积，即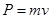，动量是矢量，动量的方向就是物体运动的方向，D正确

本题难度：简单