1、选择题  两质量均为M的冰船A、B静止在光滑冰面上，轴线在一条直线上，船头相对，质量为m的人从A船跳入B船，又立刻跳回，A、B两船最后的速度之比是（　　）
A.（M＋m）/M        B. M/(2M-m)        C.M/(M+m)      D. M/(M-m)

参考答案：C

本题解析：设人跳的速度为v，人从A船跳入B船时，根据动量守恒定律对A船和人有，对人和B船有mv=（m+M），当人从B船跳入A船时，根据动量守恒定律对B船和人有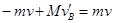，得到，对人和A船有-mv-mv=（m+M），得到
，即，C对，ABD错。

本题难度：一般

2、选择题  A、B两物体的质量之比为ma∶mb=1∶2.用质量不计的弹簧把它们连接起来，放在光滑水平面上，A物体靠在固定板上，如图所示.用力向左推B物体，压缩弹簧，当外力做功为W时，突然撤去外力，从A物体开始运动以后，弹簧弹性势能的最大值是（?）

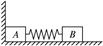
A.W/3? B.W/2? C.2W/3? D.W

参考答案：A

本题解析：由功能关系知撤去外力时，系统的机械能为W，A物体开始运动后，A、B及弹簧这一系统的机械能守恒，动量守恒，且A、B具有相等速度时，弹簧弹性势能最大.
则由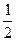mBv12="W?" ①
mBv1="(mA+mB)v?" ②
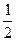mBv12-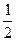(mA+mB)v2="Ep?" ③
由①②③得Ep=W.

本题难度：简单

3、简答题  如图5-1-8所示,光滑平行导轨仅其水平部分处于竖直向上的匀强磁场中,一根长为2 m的金属杆cd静止在水平轨道JK上,另一根质量为m的金属杆ab从斜轨高为h处由静止开始下滑,运动中两杆始终与轨道垂直且接触良好,两杆之间未发生碰撞.已知左边水平轨道的宽度是右边水平轨道宽度的两倍,在ab杆离开NQ前,两杆都做匀速运动,且磁场的磁感应强度大小为B.求两杆匀速时的速率.

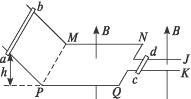
图5-1-8

参考答案：?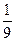

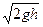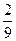
本题解析：ab杆进入水平轨道之后,切割磁感线产生感应电动势,在回路中产生电流,cd杆在安培力作用下开始运动.在两者达匀速之前,ab杆做加速度减小的减速运动,而cd杆做加速度减小的加速运动,当两者都匀速时,设ab、cd杆的速率分别为v1、v2,则ab杆产生的感应电动势E1=BLabv1?①
cd杆产生的感应电动势E2=BLcdv2?②
由于都做匀速运动,则E1=E2?③
取水平向右为正方向,在ab杆进入水平轨道到达匀速过程中,由动量定理得,
-BLabt=mv1-mv?④
在cd杆由静止到刚开始匀速过程中,由动量定理得:BLcdt=2mv2?⑤
在ab下滑高度h时,设其速度为v,有mgh=mv2?⑥
且Lab=2Lcd?⑦
解以上各式得:v1=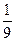
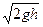
v2=.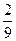

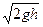本题难度：简单

4、简答题  平静的湖面上浮着一只长L="6" m、质量为550 kg的船，船头上站着一质量为m="50" kg的人，开始时，人和船均处于静止.若船行进时阻力很小，问当人从船头走到船尾时，船将行进多远？

参考答案：0.5 m?

本题解析：以人和船组成的系统为研究对象.因船行进时阻力很小，船及人所受重力与水对船的浮力平衡，可以认为人在船上行走时系统动量守恒.开始时人和船都静止，系统总动量为零，当人在船上走动时，无论人的速度如何，系统的总动量都保持为零不变.
取人运动方向为正方向，设人对岸的速度为v，船对岸的速度为V，其方向与v相反，由动量守恒定律有0=mv+(-MV)
解得两速度大小之比为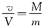
此结果对于人在船上行走过程的任一瞬时都成立.
方法一：取人在船上行走时任一极短时间为Δti，在此时间内人和船都可视为匀速运动，此时间内人和船相对地面移动的距离分别为Δsmi=viΔti和ΔsMi=ViΔti，由此有

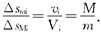
这样人从船头走到船尾时，人和船相对地面移动的总距离分别为
sm=ΣΔsmi，sM=ΣΔsMi.

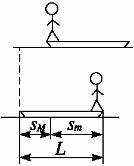
图2

由图2中几何关系可知sm+sM=L.这样，人从船头走到船尾时，船行进的距离为

代入数据有sM="0.5" m.
方法二：由于对于人在船上行走过程的任一时刻都有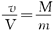
则在该过程中人和船的平均速度应满足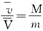
由于人和船运动时间相同，故有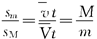
同方法一，可求得sM="0.5" m.

本题难度：简单

5、填空题  为了“探究碰撞中的不变量”，小明在光滑桌面上放有A、B两个小球．A球的质量为0.3kg，以速度8m/s跟质量为0.1kg、静止在桌面上的B球发生碰撞，并测得碰撞后B球的速度为9m/s，A球的速度变为5m/s，方向与原来相同．根据这些实验数据，小明对这次碰撞的规律做了如下几种猜想．
猜想1：碰撞后B球获得了速度，A球把速度传递给了B球．
猜想2：碰撞后B球获得了动能，A球把减少的动能全部传递给了B球．
（1）你认为以上的猜想成立吗？若不成立，请简述理由．
（2）根据实验数据，通过计算说明，有一个什么物理量，在这次碰撞中，B球所增加的这个物理量与A球所减少的这个物理量相等？

参考答案：（1）猜想1、2均不成立．因为A球的速度只减少了3m/s，B球的速度却增加了8m/s，所以猜想1是错的．
A球的动能减少了△EkA=12mv21-12mv22=5.85J，
B球动能增加了△EkB=12mBv2=4.05J，所以猜想2也是错的；
（2）计算：B球动量的增加量△pB=0.1×9=0.9kg?m/s，
A球动量的减少量△pA=0.3×8-0.3×5=0.9?kg?m/s，
从计算结果可得，B球动量的增加量与A球动量的减少量相等．即系统的总动量保持不变．
答：（1）猜想1、2均不成立．
（2）B球动量的增加量与A球动量的减少量相等．即系统的总动量保持不变．

本题解析：

本题难度：一般