1、计算题  （19分）如图所示，半径为R的四分之一圆弧形支架竖直放置，圆弧边缘C处有一小定滑轮，绳子不可伸长，不计一切摩擦，开始时，m1、m2两球静止，且m1＞m2，试求：

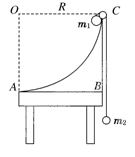
(1)m1释放后沿圆弧滑至最低点A时的速度．
(2)若A点离地高度为2R，m1滑到A点时绳子突然断开，则m1落地点离A点的水平距离是多少？
(3)为使m1能到达A点，m1与m2之间必须满足什么关系．

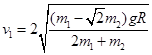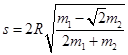参考答案：（1）（2）(3)

本题解析：（1）两个小球组成的系统机械能守恒，有：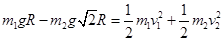
两小球在沿绳方向的速度相等，有：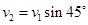
联立解得：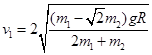
（2）绳断后m1做平抛运动，竖直方向有：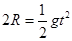
水平方向有：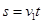
联立解得;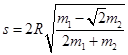
(3) 为使m1能到达A点,应满足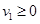
又有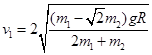
解得：

本题难度：一般

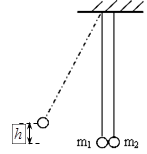
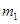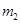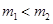2、计算题  如图，两个大小相同小球用同样长的细线悬挂在同一高度，静止时两个小球恰好接触，两个小球质量分别为和?（），现将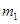拉离平衡位置，从高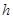处由静止释放，和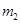碰撞后被弹回，上升高度为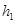，试求碰后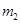能上升的高度。（已知重力加速度为g）

参考答案：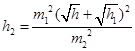

本题解析：
试题分析: 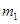碰前，由机械能守恒定律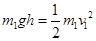：?①?得?
碰撞过程动量守恒?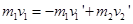?②?
碰后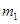反弹上升，由机械能守恒定律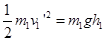：?③?
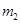上升，由机械能守恒定律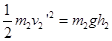：?④?
联立①—④解得?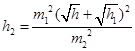

本题难度：一般

3、选择题  如图所示，将质量为2m的重物悬挂在轻绳的一端，轻绳的另一端系一质量为m的环，环套在竖直固定的光滑直杆上，光滑的轻小定滑轮与直杆的距离为d，杆上的A点与定滑轮等高，杆上的B点在A点下方距离A为d处。现将环从A处由静止释放，不计一切摩擦阻力，下列说法正确的是

A．环到达B处时，重物上升的高度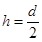
B．环到达B处时，环与重物的速度大小之比为
C．环从A到B，环减少的机械能大于重物增加的机械能
D．环能下降的最大高度为

参考答案：D

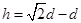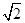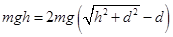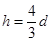本题解析：环到达B处时，重物上升的高度等于绳拉伸过来的长度，所以，A错误；环和重物在沿绳方向的速度相等，环到达B处时，环与重物的速度大小之比为，B错误；环和重物组成的系统机械能守恒，环减少的机械能等于重物增加的机械能，C错误；当环下降的高度最大时，两者速度都为零，由系统机械能守恒得，环减小的重力势能等于重物最大的重力势能，有，解得，D正确。

本题难度：一般

4、简答题  
（1）M从释放开始到第一次着地所用时间
（2）M第3次着地时系统损失的机械能与绳第3次绷直时系统损失的机械能之比
（3）M所走的全部路程（取三位有效数字）

参考答案：
（1）1s（2）△E1：△E2=4：1?（3）2.83m

本题解析：(1)从开始到M第一次着地，设着地速度为v1的过程中，对系统：
由机械能守恒定律：MgH-mgH=(M+m)v12/2?①……..（2分）
由动量定理得：?Mgt-mgt=(m+M)v1?②……..（2分）
解得：?t=1s? …………(1分)
(2)设第3次着地时的速度为v3，此时系统损失的机械能△E1即为M的动能
△E1=Mv32/2?③……….(1分)
m上升后落回速度仍为v3，绳绷直后达到共同速度v3′，损失能量△E2
绳绷直瞬间系统动量守恒，m的速度在M侧等效向上，与M同向：
m v3=(m+M) v3′?④……….(2分)
△E2=mv32/2-(m+M) v3′2/2?⑤………..(2分)
∴?△E1：△E2=4：1? ………….(1分)
(3)设M第一次着地后被m带着上升的高度为H1，
m v1=(m+M) v1′?⑥……….(1分)
MgH1-mgH1=(M+m)v1′2/2?⑦……….(2分)
解方程①⑥⑦可得?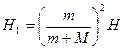?……….(2分)
依此类推可得?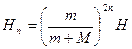?……….(2分)
M所走的全部路程为?l=H+2H1+2H1+…2Hn=2.83m? ……….(2分)

本题难度：一般

5、计算题  如图所示，物块M和m用一不可伸长的细绳通过定滑轮连接，m放在倾角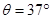的固定光滑斜面上，而穿过竖直杆PQ的物块M可沿杆无摩擦地下滑，M＝3m，开始时，将M抬高到A点，使细绳水平，此时OA段绳长为L＝4.0m，现M由静止开始下滑，求：当M下滑3.0m至B点时的速度为多大?（g取10m/s?2）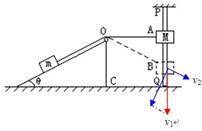

参考答案：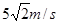

本题解析：
试卷分析：由于斜面光滑且竖直杆也光滑，所以系统机械能守恒。OA长4m，下降3m则此刻OB长度为5m，说明m物体沿斜面上升1m。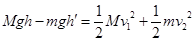，其中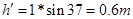由于绳子关联，所以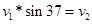则带入求解即可求得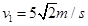
点评：此类题型考察对于系统机械能守恒定律的掌握，通过关联速度公式求解。

本题难度：一般