1、计算题 在一个水平面上建立x轴,在过原点O垂直于x轴的平面的右侧空间有一个匀强电场,场强大小E=6×105 N/C,方向与x轴正方向相同,在O处放一个带电荷量q=5×10-8 C、质量m=0.01 kg的带负电绝缘物块,物块与水平面间的动摩擦因数μ=0.2,沿x轴正方向给物块一个初速度v0=2 m/s,如图所示,求物块最终停止时的位置。(g取10 m/s2)

参考答案:解:第一个过程:物块向右做匀减速运动到速度为0,则:
f=μmg
F=qE
 =5 m/s2
=5 m/s2
x1=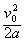 =0.4 m
=0.4 m
第二个过程:物块向左做匀加速运动,离开电场后做匀减速运动直到停止
由动能定理得:Fx1-f(x1+x2)=0
得x2=0.2 m
则物块停止在原点O左侧0.2m处
本题解析:
本题难度:一般
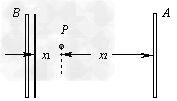
2、计算题 有一带负电的小球,其带电量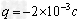 。如图所示,开始时静止在场强E=200N/C的匀强电场中的P点,靠近电场极板处有一档板s,小球与档板s的距离x1=5cm,与A板距离x2=45cm,小球的重力不计。在电场力作用下小球向左运动,与档板s相碰后电量减少到碰前的K倍,已知
。如图所示,开始时静止在场强E=200N/C的匀强电场中的P点,靠近电场极板处有一档板s,小球与档板s的距离x1=5cm,与A板距离x2=45cm,小球的重力不计。在电场力作用下小球向左运动,与档板s相碰后电量减少到碰前的K倍,已知 ,而碰撞过程中小球的机械能不损失。
,而碰撞过程中小球的机械能不损失。
(1)设匀强电场中档板s所在位置的电势为0,则电场中P点的电势为多少?小球的电势能多大?
(2)小球经过多少次碰撞后,才能运动到A板?
参考答案:(1 ) ,
, ,
, ?
?
?(2)13次
本题解析:
本题难度:一般
3、计算题 如图所示,两平行金属板E、F之间电压为U,两足够长的平行边界MN、PQ区域内,有垂直纸面向外的匀强磁场,磁感应强度为B.一质量为m、带电量为+q的粒子(不计重力),由E板中央处静止释放,经F板上的小孔射出后,垂直进入磁场,且进入磁场时与边界MN成60°角,最终粒子从边界MN离开磁场.求:
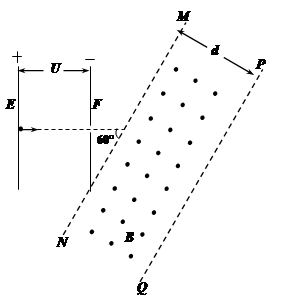
(1)粒子离开电场时的速度大小v;
(2)粒子在磁场中圆周运动的半径r和运动的时间t.
(3)两边界MN、PQ的最小距离d;
参考答案:(1)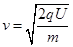 (2)4
(2)4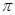 m/3qB(3)
m/3qB(3)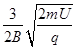
本题解析:
 (1)设粒子离开电场时的速度为v,由动能定理有:qu=mv2/2?
(1)设粒子离开电场时的速度为v,由动能定理有:qu=mv2/2?
解得: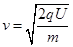 ?
?
(2)粒子离开电场后,垂直进入磁场,由洛仑兹力提供向心力有:qBv= mv2/r?
联立解得: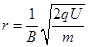 ?
?
粒子在磁场中做圆周运动的周期T=2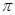 r/v?
r/v?
联立解得:T=2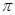 m/qB
m/qB
粒子在磁场中运动的时间t=2400/3600? T=4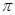 m/3qB?
m/3qB?
(3)最终粒子从边界MN离开磁场,需满足:d≧r+rsin300?
联立④⑤解得:d≧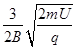 ?
?
两边界MN、PQ的最小距离d为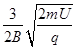
本题难度:一般
4、选择题 如图所示,在粗糙的足够长的竖直木杆上套有一个带正电小球,整个装置处在有水平匀强电场和垂直于纸面向里的匀强磁场组成的足够大的复合场中,小球由静止开始下滑,在整个运动过程中,关于描述小球运动的v-t图像中正确的是

参考答案:C
本题解析:在小球下滑的过程中,对小球受力分析,受到向下的重力mg、水平向左的电场力qE、水平向右的洛伦兹力qvB、向上的摩擦力f,还有木杆对小球的水平方向的支持力N,开始时,速度较小,qvB较小,N较大,随着速度的增加,N在减小,由f=μN可知f减小,竖直方向的合力增加,加速度增加;当速度增加到一定的程度,qvB和qE相等,此时N为零,f为零,加速度为g,达到最大;速度继续增加,N要反向增加,f增加,竖直方向上的合力减小,加速度减小,当f与mg相等时,竖直方向上的加速度为零,速度达到最大.所以选项C所示的v-t图象符合所分析的运动规律,C选项符合.
本题难度:一般
5、选择题 如图4所示,一个绝缘光滑半圆环轨道放在竖直向下的匀强电场E中,在环的上端,一个质量为m、带电荷量为+q的小球由静止开始沿轨道运动,则( ? )
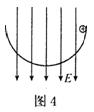
A.小球运动过程中机械能守恒
B.小球经过环的最低点时速度最大
C.在最低点球对环的压力为(mg+qE)
D.在最低点球对环的压力为3(mg+qE)
参考答案:BD
本题解析:
本题难度:简单