1、计算题 (9分)在某颗星球表面上,宇航员用弹簧秤称得质量为 的砝码的重为F,宇航员乘宇宙飞船在靠近该星球表面附近空间飞行时,测得其环绕该星球周期是
的砝码的重为F,宇航员乘宇宙飞船在靠近该星球表面附近空间飞行时,测得其环绕该星球周期是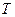 。根据上述字母符号求出该星球的质量(万有引力常量为G)
。根据上述字母符号求出该星球的质量(万有引力常量为G)
参考答案: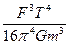
本题解析:略
本题难度:简单
2、计算题 两颗靠得很近的天体称为双星,它们以两者连线上某点为圆心作匀速圆周运动,这样就不至于由于万有引力而吸引在一起,设A、B双星质量分别为m和3m。两星间距为L,在相互万有引力的作用下,绕它们连线上某点O转动,则
(1)O和A的间距为多少?
(2)它们运动的周期为多少?
参考答案:(1)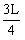
(2)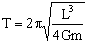
本题解析:
本题难度:一般
3、选择题 某同学在研究性学习中记录了一些与地球、月球有关的数据数据如表中所示,利用这些数据来计算地球表面与月球表面之间的距离s,则下列运算公式中错误的是
地球半径
| R=6400km
|
月球半径
| r=1740km
|
地球表面重力加速度
| g0=9.80m/s2
|
月球表面重力加速度
| g′=1.56m/s2
|
月球绕地球转动的线速度
| v=1km/s
|
月球绕地球转动周期
| T=27.3天
|
光速
| c=2.998×105 km/s
|
用激光器向月球表面发射激光光束,经过约t=2.565s接收到从月球表面反射回来的激光信号
|
?
A.s=c·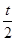 ?
?
B.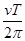 -R-r
-R-r
C.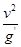 -R-r
-R-r
D.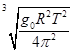 -R-r
-R-r
参考答案:C
本题解析:激光器做一次往复运动所需时间为t,由匀速直线运动s=vt可知地球表面与月球表面之间的距离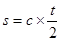 ,A对;由线速度公式
,A对;由线速度公式 为地球球心到月球球心间的距离,因此地球表面与月球表面之间的距离
为地球球心到月球球心间的距离,因此地球表面与月球表面之间的距离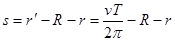 ,B对;
,B对;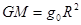 ,由万有引力提供向心力
,由万有引力提供向心力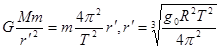 ,D对;故选C
,D对;故选C
点评:本题难度中等,天体运动这一部分公式较多,各公式间又能相互推导,需要大量的做练习题才能熟练掌握
本题难度:一般
4、选择题 物理学的发展丰富了人类对物质世界的认识,推动了科学技术的创新和革命,促进了物质生产的繁荣与人类文明的进步,下列表述不正确的是(?)
A.牛顿发现了万有引力定律,但没能测出引力常量
B.引力常量的大小等于两个质量为1kg的物体相距1m时的相互吸引力
C.以牛顿运动定律为基础的经典力学适用于研究“神舟9号”飞船的高速发射
D.万有引力定律的发现解释了天体运动的规律,并预言了海王星的存在
参考答案:B
本题解析:牛顿在前人的工作的基础上总结发现了万有引力定律,并由库仑利用扭秤实验测量出了引力常量,故选项A正确;引力常量是计算万有引力时需要一个重要的常量,没有具体的物理意义,故选项B错误;“神州9号”飞船发射时速度比较小,适用于经典力学范围,故选项C正确;万有引力定律的发现解释了天体运动的规律,根据万有引力定律和对天王星轨道的观察计算,预言了海王星的存在,故选项D正确.
本题难度:简单
5、简答题 如图所示为宇宙中一个恒星系的示意图,其中A为该星系中的一颗行星,它绕中央恒星O运行的轨道近似为圆.天文学家观测得到A行星运行的轨道半径为r,周期为T.已知万有引力常量G.
(1)求A行星做匀速圆周运动的向心加速度大小;
(2)求中央恒星O的质量;
(3)若中央恒星是半径为R的均匀球体,要使在此恒星表面被平抛出的物体不再落回恒星表面,通过计算说明抛出物体的速度需要满足什么条件.
参考答案:(1)根据圆周运动的向心加速度的表达式得出:
A行星绕恒星做匀速圆周运动的加速度大小为:a=ω2r=4π2rT2
(2)A行星绕恒星O做匀速圆周运动,设A行星和恒星的质量分别为m和M,根据万有引力定律和牛顿第二定律有:GMmr2=m4π2T2r
解得:M=4π2r3GT2.
(3)当水平抛出物体的速度大小等于或大于物体在靠近恒星表面,绕恒星做匀速圆周运动速度大小时,物体将不再落回恒星表面.设物体在靠近恒星表面,绕恒星做半径为R的匀速圆周运动的速度大小为υ,也就是我们所说的第一宇宙速度,根据万有引力定律和牛顿第二定律有:GMmR2=mυ2R,v=
本题解析:
本题难度:一般