1、简答题  如图所示，有一与竖直方向夹角为45°的直线边界，其左下方有一正交的匀强电磁场.磁场方向垂直于纸面向里，磁感应强度大小为B；电场方向竖直向上，场强大小为E=mg/q.一质量为m，电荷量为+q的小球从边界上N点正上方高为h处的M点静止释放，下落到N点时小球瞬间爆炸成质量、电荷量均相等的A、B两块.已知爆炸后A向上运动，能达到的最大高度为4h；B向下运动进入电磁场区域.此后A也将进入电磁场区域，

求：
(1)B刚进入电磁场区域的速度vB1
(2)B第二次进入电磁场区域的速度vB2
(3)设? B、A第二次进入电磁场时，与边界OO"交点分别为P、Q，求PQ之间的距离.

参考答案：（1）4?（2）v2==vB1=4
设v2与水平成α角，则tanα＝="2" (3) +48

本题解析：(1)设小球运动到N点时速度为v0，


则有mgh=mvv0=…………①…………(2分)
设爆炸后瞬间A的速度为vA1则有：?v=g?4h
即vA1＝2v0=………②…………(1分)
爆炸前后动量守恒，有mv0=vB1-vA1………③…………(1分)
联立①②③得vB1=4v0=4…………(2分)
(2)进入电磁场后由于g=E，故B做匀速圆周运动，B离开电磁场后做平抛运动，设运动时间为t，则有：
—CPsin45°＝vB1t………④…………(1分)
—CPcos45°＝gt2………⑤…………(1分)
联立④⑤得t=………⑥所以vy=gt=2vB1
由图知：v2==vB1=4…………(2分)
设v2与水平成α角，则tanα＝=2…………(2分)
(3)设运动半径为RB，有vB1B=?(2分)即RB=
故NC的距离为：—NC=RB=⑦…………(2分)
将⑥代入④得—CP=⑧…………(2分)
所以B第一次进入磁场到第二次进入磁场之间的距离为：
—NP=—NC+—CP=+=+64⑨…………(1分)
同理A第一次进入磁场到第二次进入磁场之间的距离为
—NQ=—ND+—DQ=+=+16⑩…………(1分)
故PQ间的距离为：—PQ=—NP-—NQ=+48…………(2分)

本题难度：一般

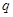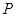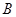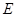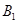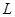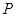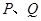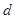2、计算题  某探究小组设计了一个质谱仪，其原理如图所示.一束电量均为，质量不同的带负电的粒子，经过电场加速后进入一速度选择器，从点进入一等腰直角三角形的有界磁场中，又从斜边射出.速度选择器中垂直纸面向里的匀强磁场的磁感应强度为，竖直向下的匀强电场强度为，有界磁场的磁感应强度为，直角边长为，为斜边的中点，两点相距为.求：

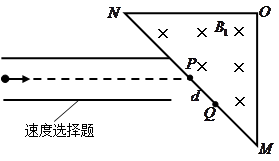
（1）带电粒子进入有界磁场的速度大小.
（2）带电粒子质量应满足的条件.
（3）打在斜边上Q点的带电粒子在磁场中运动的时间.

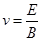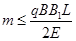参考答案：（1）?（2）?（3）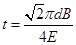

本题解析：（1）设速度为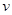，在速度选择器中，有：?①　　（3分）
带电粒子进入有界磁场的速度为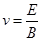　　　②（2分）
（2）设带电粒子质量为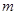，在有界磁场中做圆周运动半径为，
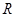根据牛顿第二定律有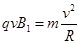；　　　③　（3分）
要使带电粒子从斜边射出，必有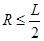　④　（2分）
由②③④得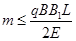：?　⑤　　　?（2分）
（3）根据几何关系可得，带电粒子在磁场中运动的半径为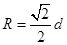?⑥　　（2分）
带电粒子在磁场中运动的周期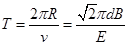：?⑦　　（2分）
带电粒子在磁场中运动的时间为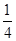周期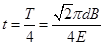：　⑧　　（2分）

本题难度：一般

3、计算题  (10分)如图所示，两根平行且光滑的金属轨道固定在斜面上，斜面与水平面之间的夹角，轨道上端接一只阻值为R=0.4的电阻器，在导轨间存在垂直于导轨平面的匀强磁场，磁场的磁感应强度B=0．5 T，两轨道之间的距离为L=40cm，且轨道足够长，电阻不计。现将一质量为m="3" g，有效电阻为r=1.0的金属杆ab放在轨道上，且与两轨道垂直，然后由静止释放，求：

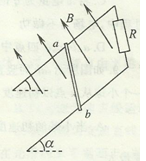
(1)金属杆ab下滑过程中可达到的最大速率；
(2)金属杆ab达到最大速率以后，电阻器R每秒内产生的电热。

参考答案：（1）（2）5.76×10-3

本题解析：（1）释放后，沿斜面方向受到重力向下的分力和安培力，当达到最大速率vm时，加速度0，根据牛顿第二定律得
安?2分
根据法拉第电磁感应定律此时? 1分
根据闭合电路欧姆定律，? 1分
根据安培力公式??1分
解得??1分
（2） 根据能的转化和守恒定律，达到最大速度后，电路中产生的焦耳热就等于重力做的功，电路中每秒钟产生的热量为
?2分
金属杆每秒钟产生的热量为?=5.76×10-3?2分

本题难度：一般

4、简答题  空间某区域有相互平行的匀强电场和匀强磁场，已知电场强度E，方向竖直向下，磁场在图中未画出，现由上向下观察一带电的单摆沿顺时针做匀速圆周运动，并且在t时间内运行了n周，已知小球的质量为m，摆线长为L，重力加速度为g，试求：
（1）小球带何种电荷，电量是多少？
（2）磁感应强度B的大小和方向？
（3）若突然撤去匀强磁场，小球将做什么运动？绳中的张力是多大？

参考答案：（1）负电荷，q=mg/E。
（2），方向向下。
（3）小球做圆周运动，。

本题解析：本题考查了考生综合应用知识分析解决问题的能力。这类问题的关键在于通过受力分析、运动过程的分析，找出临界状态及临界条件进行求解。（1）小球做匀速圆周运动所需向心力是变力，说明重力与电场力是二力平衡的，只有洛仑兹力提供向心力。mg=Eq，则q=mg/E，为负电荷所受电场力才是向上的。
（2）洛仑兹力提供向心力得：，则。
（3）突然撤去匀强磁场，洛仑兹力消失，重力与电场力仍是平衡的，小球将沿瞬时速度方向做离心运动，但由于有长为L轻绳的约束，应该是以L为半径做匀速圆周运动。瞬时速度为
，
据绳的拉力提供向心力得。

本题难度：一般

5、选择题  如图所示，在Oxyz坐标系所在的空间中，可能存在着匀强电场E或匀强磁场B，也可能两者都存在．现有一质量为m、电荷量为q的正点电荷沿z轴正方向射入此空间，发现它做速度为v0的匀速直线运动．若不计此点电荷的重力，则下列关于电场E和磁场B的分布情况中有可能的是（　　）
A．E≠0，B=0，且E沿z轴正方向或负方向
B．E=0，B≠0，且B沿x轴正方向或负方向
C．E≠0，B≠0，B沿x轴正方向，E沿y轴正方向
D．E≠0，B≠0，B沿x轴正方向，E沿y轴负方向