微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
1、计算题 如图所示,螺线管横截面积为S,线圈匝数为N,电阻为R1,管内有水平向左的变化磁场。螺线管与足够长的平行金属导轨MN、PQ相连并固定在同一平面内,与水平面的夹角为q,两导轨间距为L。导轨电阻忽略不计。导轨处于垂直斜面向上、磁感应强度为B0的匀强磁场中。金属杆ab垂直导轨,杆与导轨接触良好,并可沿导轨无摩擦滑动。已知金属杆ab的质量为m,电阻为R2,重力加速度为g。忽略螺线管磁场对金属杆ab的影响、忽略空气阻力。

(1)为使ab杆保持静止,求通过ab的电流的大小和方向;
(2)当ab杆保持静止时,求螺线管内磁场的磁感应强度B的变化率;
(3)若螺线管内方向向左的磁场的磁感应强度的变化率DB/Dt=k(k>0)。将金属杆ab由静止释放,杆将沿斜面向下运动。求当杆的速度为v时,杆的加速度大小。
参考答案:(1)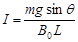 ,电流方向为由b到a(2)
,电流方向为由b到a(2) (3)
(3)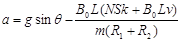
本题解析:(1)以金属杆ab为研究对象,根据平衡条件?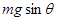 - B0I L=0(1分)
- B0I L=0(1分)
得 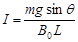 ?(1分)
?(1分)
通过ab杆电流方向为由b到a(或在图中标出)?(1分)
(2)根据法拉第电磁感应定律  (1分)
(1分)
根据欧姆定律?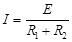 ?(1分)
?(1分)
得: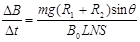 ?(1分)
?(1分)
(3)根据法拉第电磁感应定律 ?(1分)
?(1分)
ab杆切割磁感线产生的电动势 E2 = B0Lv?(1分)
总电动势? E总 = E1 + E2
感应电流?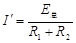 ?(1分)
?(1分)
根据牛顿第二定律?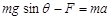 ?(1分)
?(1分)
安培力? F = B0 I′L?(1分)
所以?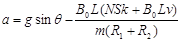 ?(1分)
?(1分)
本题难度:一般
2、选择题 在图示光滑轨道上,小球滑下经平直部分冲上圆弧部分的最高点A时,对圆弧的压力为mg,已知圆弧半径为R,则(?)

A.在最高点A,小球受重力和向心力
B.在最高点A,小球受重力和圆弧的压力
C.在最高点A,小球的速度为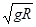
D.在最高点A,小球的向心加速度为g
参考答案:B
本题解析:在圆弧最高点A,小球受重力和轨道对小球的弹力,根据牛顿第二定律得: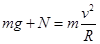 ,解得:
,解得: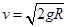 .故A、C错误,B正确.根据
.故A、C错误,B正确.根据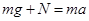 ,则小球的向心加速度为:
,则小球的向心加速度为: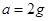 .故D错误.
.故D错误.
本题难度:简单
3、选择题 一条不可伸长的轻绳跨过质量可忽略不计的定滑轮,绳的一端系一质量m=15kg的重物,重物静止于地面上,有一质量为10Kg的猴子,从绳子的另一端沿绳向上爬,不计滑轮磨擦,在重物不离开地面的条件下,猴子向上爬的最大加速度为(g取10m/s2)
[? ]
A.25m/s2
B.10m/s2
C.5m/s2
D.15m/s2
参考答案:C
本题解析:
本题难度:一般
4、简答题 如图所示,质量为70kg的工人站在岸边通过一滑轮组打捞一块沉没在水池底部的石材,该滑轮组中动滑轮质量为5kg.当工人用120N的力拉滑轮组的绳端时,石材仍沉在水底不动.工人继续增大拉力将石材拉起,在整个提升过程中,石材始终以0.2m/s的速度匀速上升.在石材还没有露出水面之前滑轮组的机械效率为η1,当石材完全露出水面之后滑轮组的机械效率为η2,且η1:η2=63:65.绳重及滑轮的摩擦均可忽略不计,石材的密度
ρ石=2.5×103kg/m3,取g=10N/kg,求:
(1)当人用120N的力拉绳端时,岸边地面对人的支持力为多大;
(2)在石材脱离水池底部至完全露出水面的过程中,地面对人的支持力的最大值与最小值之比;
(3)当石材露出水面之前,人拉绳子的功率;
(4)此人用这个滑轮组提升重物的最大机械效率.
参考答案:
工人的重力:
G人=m人g=70kg×10N/kg=700N,
动滑轮的重力:
G动=m动g=5kg×10N/kg=50N,
未露出水面滑轮组的机械效率:
η=W有W总=(G石-F浮)h?(G石-F浮+G动)h=G石-F浮G石-F浮+G动,
露出水面后滑轮组的机械效率:
η=W有W总=G石h?(G石+G动)h=G石G石+G动,
∵η1:η2=63:65,
即ρ石Vg-ρ水Vgρ石Vg-ρ水Vg+50N:ρ石Vg?ρ石Vg+50N=63:65,
将石块的密度和水的密度代入求得:
V石=0.04m3,
石块的重力:
G石=m石g=ρ石V石g=2.5×103kg/m3×10N/kg×0.04m3=1000N,
(1)地面对人的支持力:
F=G人-F拉=700N-120N=580N;
(2)石材在水中,受到水的浮力,此时人的拉力最小,地面对人的支持力最大,
石材受到的浮力:
F浮=ρ水V排g=1×103kg/m3×10N/kg×0.04m3=400N,
F拉1=13 (G石+G动-F浮)=13(1000N+50N-400N)=6503 N,
地面的支持力:
F支1=G人-F拉1=700N-6503 N=14503 N;
石材离开水面,此时人的拉力最大,地面对人的支持力最小,
F拉2=13 (G石+G动)=13(1000N+50N)=350N,
地面的支持力:
F支2=G人-F拉2=700N-350N=350N;
F支1:F支2=14503 N:350N=29:21;
(3)当石材露出水面之前,F拉1=13(G石+G动-F浮)=13 (1000N+50N-400N)=6503 N,
v=3×0.2m/s=0.6m/s
人拉绳子的功率:
P=F拉1v=6503 N×0.6m/s=130W;
(4)重物露出水面后,滑轮组受到的向下的拉力最大,为F=G人=700N,
∵绳重及滑轮的摩擦均可忽略不计,
∴F=13(G物+G动),
∴G物=3F-G动=3×700N-50N=2050N,
η=W有W总=GhFs=GhF?3h=G3F=20503×700≈97.6%.
答:(1)当人用120N的力拉绳端时,岸边地面对人的支持力为580N;
(2)在石材脱离水池底部至完全露出水面的过程中,地面对人的支持力的最大值与最小值之比为29:21;
(3)当石材露出水面之前,人拉绳子的功率为130W;
(4)此人用这个滑轮组提升重物的最大机械效率为97.6%.
本题解析:
本题难度:一般
5、计算题 如图所示,绷紧的传送带与水平面的夹角θ=30 °,皮带在电动机的带 动下,始终保持v0=2m/s的速率运行。现把一质量为m=10kg的工件(可视为质点)轻轻放在皮带的底端,经时间1.9s,工件被传送到h=1.5m的高处,取g=10m/s2。求:
动下,始终保持v0=2m/s的速率运行。现把一质量为m=10kg的工件(可视为质点)轻轻放在皮带的底端,经时间1.9s,工件被传送到h=1.5m的高处,取g=10m/s2。求:
(1)工件与皮带间的动摩擦因数;
(2)工件相对传送带运动的位移。

参考答案:解:(1)由题意得,皮带长为:L= =3m。工件速度达到v0之前,从静止开始做匀加速运动,设匀加速运动的时间为t1,位移为s1,有:s1=
=3m。工件速度达到v0之前,从静止开始做匀加速运动,设匀加速运动的时间为t1,位移为s1,有:s1=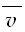 t1=
t1= t1
t1
设工件最终获得了与传送带相同的速度,则达到v0之后工件将做匀速运动,有:L-s1=v0(t-t1)
解得:t1=0.8s<1.9s,故假设工件最终获得与传送带相同的速度正确。
加速运动阶段的加速度为:a=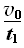 =2.5 m/s2
=2.5 m/s2
在加速运动阶段,根据牛顿第二定律,有:
μmgcosθ-mgsinθ=ma
解得:μ=0.866
(2)在时间t1内,传送带运动的位移为:
s=v0t1=1.6m
s1=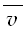 t1=
t1= t1=0.8m。
t1=0.8m。
所以工件相对传送带的位移为:△s=s-s1=0.8m
本题解析:
本题难度:一般