微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
1、选择题 如图所示,质量为m、带电量为+q的三个相同的带电小球A、B、C,从同一高度以初速度v0水平抛出,B球处于竖直向下的匀强磁场中,C球处于垂直纸面向里的匀强电场中,它们落地的时间分别为tA、tB、tC,落地时的速度大小分别为vA、vB、vC,则以下判断正确的是:

A.tA=tB=tC? B.tA=tC>tB
C.vB>vA=vC? D.vA<vB<vC
参考答案:A
本题解析:AB、由题意可知,A球只受重力做平抛运动,竖直方向为自由落体,B球除受重力之外,还受垂直纸面向里的洛伦兹力作用,竖直方向只受重力作用,做自由落体运动,C球除受重力之外,还受垂直纸面向里的电场力作用,竖直方向只受重力作用,做自由落体运动,可见三球竖直方向都做自由落体运动,高度相同,则它们落地的时间相同;A正确
CD、A球只有重力做功;B球虽然还受洛伦兹力作用,但洛伦兹力不做功,也只有重力做功;C球除重力做功外,电场力对其做正功,根据动能定理可知:A、B两球合力做的功相等,初速度又相同,所以末速度大小相等,而C球合外力做的功比A、B两球合外力做的功大,而初速度与A、B球相等,故C球的末速度比A、B两球大,即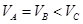 ;错误
;错误
故选A
点评:注意对物体受力情况的分析,要灵活运用运动的合成与分解,不涉及到运动过程的题目可以运用动能定理去解决,简洁、方便。
本题难度:一般
2、选择题 用一金属窄片折成一矩形框架水平放置,框架右边上有一极小开口。匀强磁场的磁感应强度大小为B,方向垂直于纸面向里,如图所示,框架以速度v1向右匀速运动,一带电油滴质量为m,电荷量为q,以速度v2从右边开口处水平向左射入,若油滴恰能在框架内做匀速圆周运动,则

[? ]
A.油滴带正电,且逆时针做匀速圆周运动
B.油滴带负电,且顺时针做匀速圆周运动
C.圆周运动的半径一定等于
D.油滴做圆周运动的周期等于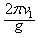
参考答案:BD
本题解析:
本题难度:一般
3、简答题 如图所示,在直角坐标系的I、Ⅱ象限内有垂直于纸面向里的匀强磁场,第Ⅲ象限有沿y轴负方向的匀强电场,第Ⅳ象限内无电场和磁场。质量为m,电荷量为q的粒子由M点以速度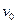 沿x轴负方向进入电场,不计粒子的重力,粒子经N和x轴上的P点最后又回到M点。设OM=OP =l,ON=2l,求:
沿x轴负方向进入电场,不计粒子的重力,粒子经N和x轴上的P点最后又回到M点。设OM=OP =l,ON=2l,求:
(1)电场强度E的大小;
(2)匀强磁场磁感应强度B的大小;
(3)粒子从M点进入电场,经N、P点最后又回到M点所用的时间t。
参考答案:见解析
本题解析:(1)根据粒子在电场中的运动情况可知,粒子带负电,粒子在电场中运动所用的时间设为
在x方向有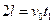 ?①
?①
在y方向有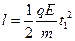 ?②
?②
解得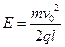 ?③
?③
(2)设粒子到达N点的速度为v,运动方向与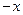 轴夹角
轴夹角
由动能定理得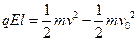 ?④
?④
将③式代入,得

粒子在磁场中做匀速圆周运动,经过P点时的速度方向也与负x方向成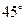 ,从P到M做直线运动,NP=NO+OP=3l
,从P到M做直线运动,NP=NO+OP=3l
粒子在匀强磁场中在洛伦兹力的作用下做匀速圆周运动,
半径为
联立上述各式解得
(3)粒子在电场中运动所用时间为
粒子在磁场中所用时间为
由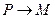 匀速直线运动所用时间
匀速直线运动所用时间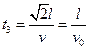
粒子从M进入电场,经N、P点最后又回到M点所用的时间
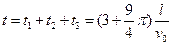 .
.
本题难度:一般
4、计算题 (14分)如图13所示,在平面直角坐标系 中,仅在第Ⅱ象限存在沿
中,仅在第Ⅱ象限存在沿 轴正方向的匀强电场,一质量为
轴正方向的匀强电场,一质量为 ,电荷量为
,电荷量为 ,可视为质点的带正电粒子(重力不计)从
,可视为质点的带正电粒子(重力不计)从 轴负半轴
轴负半轴 处的M点,以初速度
处的M点,以初速度 垂直于
垂直于 轴射入电场,经
轴射入电场,经 轴上
轴上 处的P点进入第I象限。
处的P点进入第I象限。
(1)求电场强度的大小和粒子进入第I象限的速度大小。
(2)现要在第I象限内加一半轻适当的半圆形匀强磁场区域,使(1)问中进入第I象限的粒子,恰好以垂直于 轴的方
轴的方 向射出磁场。求所知磁场区域的半径。要求;磁场区域的边界过坐标原点,圆心在
向射出磁场。求所知磁场区域的半径。要求;磁场区域的边界过坐标原点,圆心在 一上,磁场方向垂直于从标平面向外,磁感应强度为
一上,磁场方向垂直于从标平面向外,磁感应强度为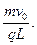

参考答案:(1)
(2)
本题解析:
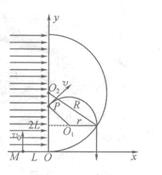
解:(1)设粒子到达P点用时为
 方向:
方向: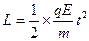 ?(2分)
?(2分)
 方向:
方向: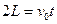 ?(1分)
?(1分)
解得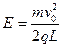 ?(1分)
?(1分)
又由动能定理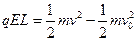 ?(2分)
?(2分)
解得 ?(1分)
?(1分)
(2)粒子进入磁场,速度方向与 方向夹角
方向夹角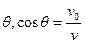 ,
,
得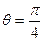 ?(1分)
?(1分)
设粒子在磁场中运动的半径为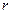 ,
,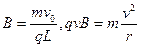 ,
,
及
解得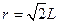 ?(2分)
?(2分)
如图,设磁场区域半径为R根据勾股定理
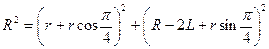 ?(2分)
?(2分)
解得 ?(2分)
?(2分)
本题难度:简单
5、计算题 如图所示,第四象限内有互相正交的匀强电场E与匀强磁场B1, E的大小为0.5×103V/m, B1大小为0.5T;第一象限的某个矩形区域内,有方向垂直纸面向里的匀强磁场B2,磁场的下边界与x轴重合.一质量m=1×10-14kg、电荷量q=1×10-10C的带正电微粒以某一速度v沿与y轴正方向60°角从M点沿直线运动,经P点即进入处于第一象限内的磁场B2区域.一段时间后,小球经过y轴上的N点并与y轴正方向成60°角的方向飞出。M点的坐标为(0,-10),N点的坐标为(0,30),不计粒子重力, g取10m/s2.
(1)请分析判断匀强电场E1的方向并求出微粒的运动速度v;
(2)匀强磁场B2的大小为多大?;
(3) B2磁场区域的最小面积为多少?
参考答案:(1)由于重力忽略不计,微粒在第四象限内仅受电场力和洛伦兹力,且微粒做直线运动,速度的变化会引起洛仑兹力的变化,所以微粒必做匀速直线运动.这样,电场力和洛仑兹力大小相等,方向相反,电场E的方向与微粒运动的方向垂直,即与y轴负方向成30°角斜向下.(2分)?
由力的平衡有
Eq=B1qv
∴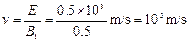 ?(2分)?
?(2分)?
(2)画出微粒的运动轨迹如图.
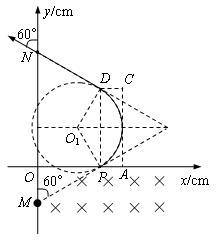
由几何关系可知粒子在第一象限内做圆周运动的半径为
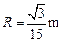 (2分) ?
(2分) ?
微粒做圆周运动的向心力由洛伦兹力提供,即
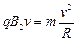 (2分) ?
(2分) ?
解之得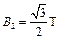 ?(2分)?
?(2分)?
(3)由图可知,磁场B2的最小区域应该分布在
图示的矩形PACD内.由几何关系易得
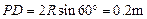 (2分)
(2分)
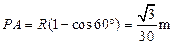 (2分)
(2分)
所以,所求磁场的最小面积为
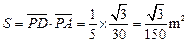 ?(2分)
?(2分)
本题解析:略
本题难度:一般