微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
1、选择题 如图,在矩形区域abcd区域中,分布有垂直纸面向外的匀强磁场,ab长为L,在ab的中点P处有一电子发射源,出射电子速率取一切可能值,所有电子出射的速度方向均与ab成30°,下列说法正确的是(? )

A.只要初速度大小取合适的值,电子可以在磁场中做完整的圆周运动
B.电子入射速度越大,在磁场中运动的时间一定越短
C.从ad边出射的电子一定比从bc出射的粒子时间长
D.当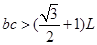 时,cd边无电子射出
时,cd边无电子射出
参考答案:CD
本题解析:粒子要做完整的圆周运动,必须还得经过P点,根据对称性可得,无论如何运动,粒子都不会再次经过P点,即无论速度大小如何,粒子都不会做完整的圆周运动,所以A错误;根据公式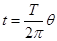 可得
可得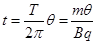 与初速度无关,B错误;根据轨迹可得从ad边出射的电子的轨迹所对圆心角大于从bc出射的圆心角,所以从ad边出射的电子一定比从bc出射的粒子时间长,C正确;当粒子轨迹与C点相切时,粒子恰好不从cd边射出,故根据几何知识可得此时bc的长度为
与初速度无关,B错误;根据轨迹可得从ad边出射的电子的轨迹所对圆心角大于从bc出射的圆心角,所以从ad边出射的电子一定比从bc出射的粒子时间长,C正确;当粒子轨迹与C点相切时,粒子恰好不从cd边射出,故根据几何知识可得此时bc的长度为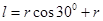 ,
,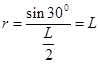 ,,解得
,,解得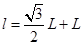 ,所以如果
,所以如果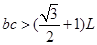 时,cd边无电子射出,D正确;
时,cd边无电子射出,D正确;
本题难度:一般
2、计算题 如图,在0≤x 区域内存在与xy平面垂直的匀强磁场,磁感应强度的大小为B,在t=0时刻,一位于坐标原点的粒子源在xy平面内发射出大量同种带电粒子,所有粒子的初速度大小相同,方向与y轴正方向的夹角分布在0~180°范围内。已知沿y轴正方向发射的粒子在t=t0时刻刚好从磁场边界上P(
区域内存在与xy平面垂直的匀强磁场,磁感应强度的大小为B,在t=0时刻,一位于坐标原点的粒子源在xy平面内发射出大量同种带电粒子,所有粒子的初速度大小相同,方向与y轴正方向的夹角分布在0~180°范围内。已知沿y轴正方向发射的粒子在t=t0时刻刚好从磁场边界上P( a,a)点离开磁场,求:
a,a)点离开磁场,求:
(1)粒子在磁场中做圆周运动的半径R及粒子的比荷q/m;
(2)此时刻仍在磁场中的粒子的初速度方向与y轴正方向夹角的取值范围;
(3)从粒子发射到全部粒子离开磁场所用的时间。
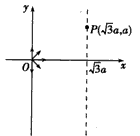
参考答案:解:(1)初速度与y轴正方向平行的粒子在磁场中的运动轨迹如图中的 所示,其圆心为C
所示,其圆心为C
由题给条件可以得出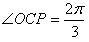 ①
①
此粒子飞出磁场所用的时间为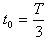 ②,式中T为粒子做圆周运动的周期
②,式中T为粒子做圆周运动的周期
设粒子运动速度的大小为v,半径为R,由几何关系可得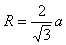 ③
③
由洛伦兹力公式和牛顿第二定律有
 ?④
?④
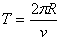 ?⑤
?⑤
联立②③④⑤式,得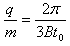
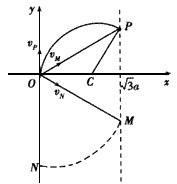
(2)依题意,同一时刻仍在磁场内的粒子到O点距离相同。在t0时刻仍在磁场中的粒子应位于以O点为圆心、OP为半径的弧MN上,如图所示

设此时位于P、M、N三点的粒子的初速度分别为vP、vM、vN。由对称性可知vP与OP、vM与OM、vN与ON的夹角均为π/3。设vM、vN与y轴正向的夹角分别为θM、θN,由几何关系有
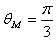 ?,
?,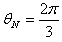
对于所有此时仍在磁场中的粒子,其初速度与y轴正方向所成的夹角θ应满足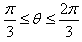
(3)在磁场中飞行时间最长的粒子的运动轨迹应与磁场右边界相切
由几何关系可知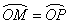
由对称性可知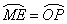
从粒子发射到全部粒子飞出磁场所用的时间tm=2t0
本题解析:
本题难度:困难
3、简答题 静止在匀强磁场中的
U,放出α粒子,衰变成Th,衰变后Th的速度方向与磁场方向垂直.
(1)写出衰变方程;
(2)计算衰变后Th的轨道半径与α粒子的轨道半径之比.
参考答案:(1)衰变的方程为:?23892U→?23490Th+?42He
②在磁场中两粒子由洛伦兹力提供粒子在磁场运动的向心力得:
?Bqv=mv2R
由上式得:R=mvBq
因?23490Th和?42He的动量等大,所在磁场相同,有:RThRHe=qHeqTh即:RThRHe=145
答:(1)衰变方程为:?23892U→?23490Th+?42He.
(2)衰变后?23490Th的轨道半径与α粒子的轨道半径之比是1:45.
本题解析:
本题难度:一般
4、选择题 如图所示,矩形MNPQ区域内有方向垂直于纸面的匀强磁场,有5个带电粒子从图中箭头所示位置垂直于磁场边界进入磁场,在纸面内做匀速圆周运动,运动轨迹为相应的圆弧,这些粒子的质量,电荷量以及速度大小如下表所示。由以上信息可知,从图中a、b、c处进入的粒子对应表中的编号分别为( ? )
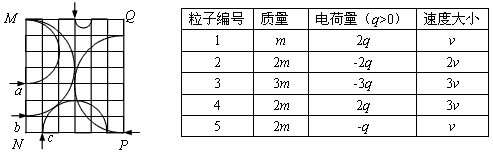
A.3、5、4
B.4、2、5
C.5、3、2
D.2、4、5
参考答案:D
本题解析:
本题难度:一般
5、计算题 一半径足够大的绝缘圆筒,筒上有一小孔。筒内有圆心在圆筒轴线上的圆形匀强磁场区域,磁场的磁感应强度为B,方向沿筒的轴线(整个装置的横截面如图)。一质量为m,带电量为q的小球(重力不计)以速度v0沿孔径方向进入圆筒内。设带电小球与筒壁碰撞后以原速率返回,碰撞时间很短,碰撞过程小球的电量不变。小球进入圆筒后,与筒壁碰撞四次后恰好又从小孔穿出,求圆筒内圆形磁场区域的半径。
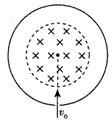
参考答案:解:设小球在磁场中的轨道半径为R

小球在磁场中运动有两种情况
(1)若运动轨迹如图甲,设磁场区域半径为r1
?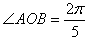
在三角形OAO1中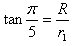
解得
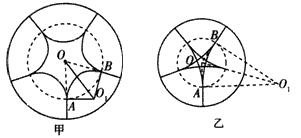
?(2)若运动轨迹如图乙,设磁场区域半径为r2
?
在三角形OAO1中
解得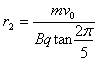
本题解析:
本题难度:困难