1、计算题  如图所示，带支架的平板小车沿水平面向左做直线运动，小球A用细线悬挂于支架前端，质量为m的物块B始终相对于小车静止地摆放在右端（B与小车间的动摩擦因数为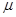）。某时刻观察到细线偏离竖直方向角，

求：此刻小车对物块B产生作用力的大小和方向

参考答案：mg，合力方向与竖直方向成θ

本题解析：设小车的加速度为a, 如图，对小球A受力分析，正交分解可得：

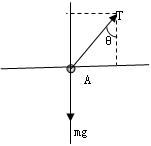
Tsinθ＝mAa?①（1分）
Tcosθ=mAg?②（1分）
联立①②解得a=gtanθ③(1分)
再对物体B受力分析如图，可知，

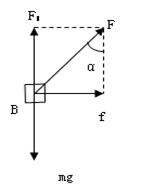
在水平方向应用牛顿第二定律得：f=ma?④(1分)
竖直方向有：FN＝mg?⑤(1分)
联立③④⑤可求得f与FN的合力F＝mg（2分）
设合力方向与竖直方向成α，则tanα=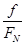=tanθ,（2分）
所以α＝θ，即合力方向与竖直方向成θ，（也可写成与水平方向成90°－θ）(1分)

本题难度：一般

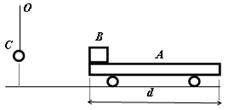
2、计算题  如图所示，质量为mA=2kg的平板车A静止在水平地面上，车长d =5m。物块B静止在平板车左端，在物块B正前方某处。有一小球C，球C通过长l = 0.32m的细绳与固定点O相连，球C恰好与物块B等高，且C始终不与平板车A接触。在t = 0时刻，平板车A突然获得水平初速度v0开始向左运动，后来某一时刻物块B与球C发生弹性碰撞，碰后球C恰好能绕O点在竖直平面内作圆周运动。若B、C可视为质点，mB=mC= 1kg，物块B与平板车A、平板车A与地面之间的动摩擦因数均为?=0.2，g取10m/s2，求：
（1）B、C碰撞瞬间，细绳拉力的大小？
（2）B、C碰撞前瞬间物块B的速度大小。
（3）若B、C碰撞时，物块B在平板车的中间位置，且t0=1.5s时平板车A的速度变为v1 =5m/s，则
物块B是在加速阶段还是减速阶段与球C相碰撞？小车的初速度v0多大？

参考答案：（1）60N（2）4m/s；（3）减速阶段与球C相碰；9m/s；

本题解析：（1）当球C在最高点处时。由牛顿第二定律，得?
碰后球C从最低点到最高点过程中：
?
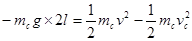当球C在最低点处：?
解得：F＝60N?
（2）物块B与球C碰撞前速度为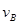，碰撞后速度为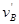，则
?
?
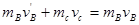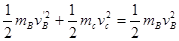解得：?
（3）刚开始时，平板车的加速度大小，物块B的加速度大小，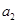
对平板车，由牛顿第二定律，?得
对物块B，??
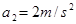假设B在加速阶段与C相碰，加速时间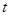，则

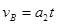
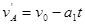,且?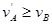
故平板车A的初速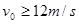度?
时平板车速度?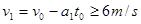
由于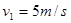?所以物块B只能在与平板车相对静止共同减速阶段与球C相碰。
物块B与平板车相对静止共同减速时加速度大小，由牛顿第二定律，得
??
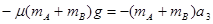设物块B与平板车速度相对滑动时间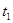，则
?
?
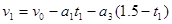联立式子，解得：

本题难度：一般

3、选择题  如图，人与重物质量相等，开始时人与重物处于同一水平高度，当人从静止起沿绳加速向上爬时，人与重物的运动情况是（不计绳的质量和滑轮摩擦）（?）

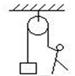
A．人加速上升，重物加速下降
B．人加速上升，重物静止不动
C．人和重物都加速上升，同时到顶
D．人与重物都加速上升，但人上升得快

参考答案：C、

本题解析：人和物体的受力均为拉力和重力，合力相同，由牛顿第二定律可知，人和物体对地的加速度相同，经过相同的时间，两者对地的位移相同，同时到顶。可得C正确。
点评：本题的关键是从人和物体的受力分析着手，得出两者的受力相同，

本题难度：简单

4、计算题  如图所示，一个静止在水平地面上A点的物体，质量是2kg，物体与地面之间的动摩擦因数为0.2，物体在大小为20N，方向与水平面成370的斜向下的推力F作用下沿水平地面从A点开始向右沿直线运动，经过2s后撤去外力F，最终物体停在某处B点，求AB之间的总距离（sin370=0.6,cos370=0.8,g=10m/s2结果保留3位有效数字）

参考答案：Fcosθ-Ff=ma1，? X1=9.6m，? X=x1+x2
FN=mg+Fsinθ? V1="9.6m/s" ?X=32.6m
FF=μFN?-μmg=ma2?
X1=at2/2 ?V2-v12=2a2x2
V1=a1t1?X2=23.0m

本题解析：略

本题难度：简单

5、简答题  质量为0.1kg的弹性球从空中某高度由静止开始下落，该下落过程对应的v-t图象如图所示．球与水平地面相碰后反弹，离开地面时的速度大小为碰撞前的2/3．该球受到的空气阻力大小恒为f，取g=10m/s2，求：
（1）弹性球受到的空气阻力f的大小；
（2）弹性球第一次碰撞后反弹的最大高度h；
（3）若弹性球与地面第一次碰撞的时间为△t′=

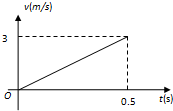
参考答案：（1）设弹性球第一次下落过程中的加速度大小为a1，由图知
a1=△v△t=30.5m/s2=6m/s2
根据牛顿第二定律，得mg-f=ma1
解得：f=m（g-a1）=0.4N
（2）由图知弹性球第一次到达地面时的速度大小为v1=3m/s，
设球第一次离开地面时的速度为v2，则
v2=23v1=2m/s
第一次离开地面后，设上升过程中球的加速度大小为a2，则mg+f=ma2
a2=14m/s2
于是，有0-v22=-2a2h
解得h=17m
（3）弹性球自由下落的距离为：H=0+v12?△t=0+32×0.5m=0.75m
（或由v-t图象所围面积求得）
第一次离开地面后，设上升到最大高度的时间为t2，则
0-v2=-a2t2
解得t2=17s…
所求过程中弹性球运动的位移大小为△x=H-h=0.75m-17m=1728m
所以所求过程中弹性球运动的平均速度大小为.v=△x△t+△t′+t2=0.85m/s
方向：竖直向下．
答：（1）弹性球受到的空气阻力f的大小为0.4N；
（2）弹性球第一次碰撞后反弹的最大高度h为17m；
（3）若弹性球与地面第一次碰撞的时间为△t′=114s，则由静止开始下落到第一次碰撞后反弹至最大高度的过程中弹性球运动的平均速度大小为0.85m/s，方向竖直向下．

本题解析：

本题难度：一般