微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
1、选择题 伽利略在研究自由落体运动时,做了如下的实验:他让一个铜球从阻力很小(可忽略不计)的斜面上由静止开始滚下,并且做了上百次.假设某次实验伽利略是这样做的:在斜面上任取三个位置A、B、C.让小球分别由A、B、C滚下,如图所示,让A、B、C与斜面底端的距离分别为s1、s2、s3,小球由A、B、C运动到斜面底端的时间分别为t1、t2、t3,小球由A、B、C运动到斜面底端时的速度分别为v1, v2、v3,则下列关系式中正确并且是伽利略用来证明小球沿光滑斜面向下运动是匀变速直线运动的是(? )
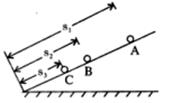
A.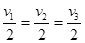 ?B.
?B.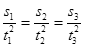
C.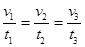 ?D.
?D.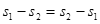
参考答案:B
本题解析:小球在斜面上三次运动的位移不同,末速度一定不同,故A错误;由运动学公式可知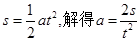 故三次下落中位移与时间平方向的比值一定为定值,伽利略正是用这一规律说明小球沿光滑斜面下滑为匀变速直线运动,故B正确;由v=at可得
故三次下落中位移与时间平方向的比值一定为定值,伽利略正是用这一规律说明小球沿光滑斜面下滑为匀变速直线运动,故B正确;由v=at可得 ,三次下落中的加速度相同,故公式正确,但是不是当时伽利略用来证明匀变速直线运动的结论;故C错误;由图可知及运动学规律可知,s1-s2>s2-s3,故D错误。
,三次下落中的加速度相同,故公式正确,但是不是当时伽利略用来证明匀变速直线运动的结论;故C错误;由图可知及运动学规律可知,s1-s2>s2-s3,故D错误。
本题难度:一般
2、计算题 (14分)从地面上以初速度v0竖直向上抛出一质量为m的球,若运动过程中受到的空气阻力与其速率v成正比关系,球运动的速率随时间变化规律如图所示,t1时刻到达最高点,再落回地面,落地时速率为v1,且落地前球已经做匀速运动,求:
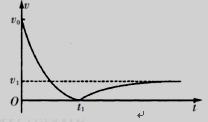
(1)球从抛出到落地过程中克服空气阻力所做的功
(2)球抛出瞬间的加速度大小;
(3)球上升的最大高度H。
参考答案:(1)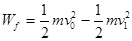 (2)
(2)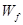 (3)
(3)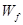
本题解析:(1)设克服空气阻力所做的功为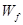
由动能定理有:
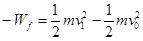 ?(1分)
?(1分)
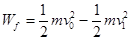 ?(1分)
?(1分)
(2)空气阻力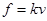 ?(1分)
?(1分)
落地前匀速运动,则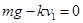 ?(2分)
?(2分)
设刚抛出时加速度大小为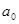
则?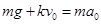 ?(2分)?
?(2分)?
解得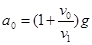 ?(1分)
?(1分)
(3)上升时加速度为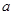 ,?
,?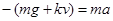 ?(1分)
?(1分)
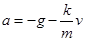 ?(1分)
?(1分)
取极短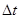 时间,速度变化
时间,速度变化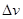 ,有:
,有:
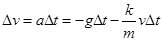 ?(1分)
?(1分)
又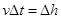 ?(1分)
?(1分)
上升全程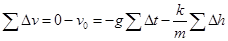 ?(1分)
?(1分)
则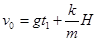
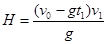 ?(1分)
?(1分)
本题难度:一般
3、选择题 一个物体从静止出发以加速度a做匀加速直线运动.经过时间t后,改作以t时刻末的速度做匀速直线运动,则在2t时间内的平均速度是?
A.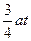
B.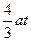
C.3at
D.
参考答案:A
本题解析:略
本题难度:简单
4、简答题 甲、乙两车,从同一地点,同时开始作同向直线运动.已知甲车以速度20m/s作匀速直线运动,乙车以初速度5m/s开始作匀加速运动,加速度为1m/s2.试分析:
(1)经过多长时间,乙车落后于甲车的距离为最大?落后的最大距离是多大?此时乙车的速度多大?
(2)经过多长时间,乙车追上甲车?此时乙车的速度多大?
参考答案:(1)当两车速度相等时,两车距离最大.
?经历的时间? t=v乙-v乙0a=20-51s=15s.
此时甲车的位移x甲=v甲t=20×15m=300m
乙车的位移x乙=v乙0t+12at2=5×15+12×1×152=187.5m.
最大距离△x=x甲-x乙=112.5m
此时乙车的速度等于甲车的速度,为20m/s.
(2)乙车追上甲车时,位移相等.
有v甲t=v乙0t+12at2,代入数据t=30s
此时乙车的速度v=v乙0+at=5+1×30m/s=35m/s.
本题解析:
本题难度:一般
5、简答题 己知O、A、B、C为同一直线上的四个点.已知AB间的距离为8m,BC间的距离为12m.一个质点从O点由静止出发,沿此直线做匀加速直线运动,依次经过A、B、C三点.己知物体通过AB段与BC段所用的时间相等.求O点与A点间的距离.

参考答案:由△s=at2可得物体的加速度a的大小为a=△st2=12-8t2=4t2
物体经过B点时的瞬时速度vB为vB=.vAC=202t
再vt2=2as可得OB两点间的距离sOB为sOB=v2B2a=100t2?t22×4m=12.5m
所以O与A间的距离sOA为sOA=sOB-sAB=(12.5-8)m=4.5m
答:O点与A点间的距离为4.5m.
本题解析:
本题难度:一般