1、计算题  如图所示，在倾角为θ的光滑斜面上有两个用轻质弹簧相连接的物块A、B，它们的质量分别为mA、mB，弹簧的劲度系数为k，C为一固定挡板．系统处于静止状态，现开始用一恒力F沿斜面方向拉物块A使之向上运动，重力加速度为g，问：

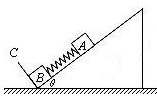
（1）物块B刚要离开C时，弹簧形变量为多少？
（2）物块B刚要离开C时，物块A的加速度多大？
（3）从开始到物块B刚要离开C时的过程中，物块A的位移多大？

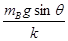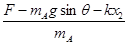参考答案：（1）（2）（3）

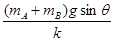
本题解析：（1）当B刚要离开C时，弹簧处于伸长状态，对B根据物体的平衡条件得：

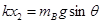
所以，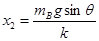
设此时A的加速度为a，对A应用牛顿第二定律有：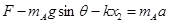
解得：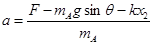
系统静止时，弹簧处于压缩状态，对A根据物体的平衡条件，弹簧的弹力大小为：

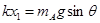
则弹簧的压缩量为：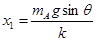
物块A的位移即为弹簧长度的改变量：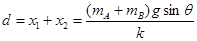

本题难度：一般

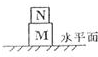
2、选择题  如图所示的四个图中，M、N两方形木块处于静止状态，它们相互之间一定没有弹力作用的是（　　）
A．

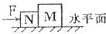
B．

C．

D．

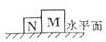
参考答案：
A、题目中要求相互之间一定没有弹力，在A中若N与地面间光滑，则N对M有弹力作用，故A错误；
B、物体M受到N的压力，N受到M的支持力，故B错误；
C、同理，若N与斜面间光滑，则N受到M沿斜面向上的弹力作用，故C错误；
D、N、M两物体由于没有相互挤压，在水平地面上各自受重力和支持力作用而处于平衡，虽然NM互相接触，但由于没有挤压作用故无弹力存在，故D错误．．
故选D

本题解析：

本题难度：一般

3、计算题  如图所示，水平光滑绝缘轨道MN的左端有一固定绝缘挡板，轨道所在空间存在水平向左、E＝4×102N/C的匀强电场。一个质量m＝0.2kg、带电荷量q＝5.0×10－5C的滑块（可视为质点），从轨道上与挡板相距x1＝0.2m的P点由静止释放，滑块在电场力作用下向左做匀加速直线运动。当滑块与挡板碰撞后滑块沿轨道向右做匀减速直线运动，运动到与挡板相距x2＝0.1m的Q点，滑块第一次速度减为零。若滑块在运动过程中，电荷量始终保持不变，求：

（1）滑块由静止释放时的加速度大小a；
（2）滑块从P点第一次达到挡板时的速度大小v；
（3）滑块与挡板第一次碰撞的过程中损失的机械能ΔE。

参考答案：（1） 0.1m/s2?（2） 0.2m/s?（3） 2×10－3J

本题解析：
试题分析: 设滑块沿轨道向左做匀加速运动的加速度为a，根据牛顿第二定律有
qE＝ma?代入数据得a＝0.1m/s2。
（2）滑块从P点运动到挡板处的过程中，由动能定理有
qEx1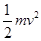＝?代入数据有v=0.2m/s。
（3）滑块第一次与挡板碰撞过程中损失的机械能等于滑块由P点运动到Q点过程中电场力所做的功，即ΔE＝qE（x1－x2）＝2×10－3J。

本题难度：一般

4、选择题  如图所示，一竖直平面内光滑圆形轨道半径为R，小球以速度v0经过最低点B沿轨道上滑，并恰能通过轨道最高点A。以下说法正确的是(? )

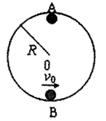
A．v0应等于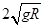，小球到A点时速度为零
B．v0应等于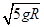，小球到A点时速度和加速度都不为零
C．小球在B点时加速度最大，在A点时加速度最小
D．小球从B点到A点，其速度的增量为(1＋)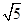

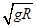
参考答案：BCD

本题解析：由于小球恰好能通过轨道的最高点，在最高点A处，根据牛顿第二定律有：mg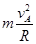＝＝maA，解得：vA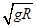＝，aA＝g，故选项A错误；在由最低点到最高点的过程中，根据机械能守恒定律有：2mgR＝－，解得：v0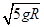＝，故选项B正确；小球在B点是重力势能最小，动能最大，在A点时重力势能最大，动能最小，因此在B点时加速度最大，在A点时加速度最小，故选项C正确；小球通过A、B两点时速度方向相反，因此在由B到A的过程中，其速度的增量为：Δv＝vA－(－v0)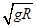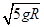＝＋＝(1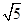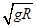＋)，故选项D正确。

本题难度：一般

5、选择题  在汽车中悬线上挂一小球．实验表明，当汽车做匀变速直线运动时，悬线将与竖直方向成某一固定角度θ，如图所示．若在汽车的光滑底板上还有一个跟其相对静止的物体M，则关于汽车的运动情况和物体M的受力情况，下列说法中正确的是（　　）
A．汽车可能向左做加速直线运动
B．汽车可能向右做加速直线运动
C．M除受到重力、底板的支持力作用外，还可能受到向右的摩擦力作用
D．M除受到重力、底板的支持力作用外，还一定受到向右的弹力作用