微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
1、简答题 物体以60J的初动能从固定斜面底端向上运动,上升到某一高度动能损失了30J,而机械能损失了10J,则返回底端时动能应为多少?
参考答案:解析:运用动能定理分析得出:物体损失的动能等于物体克服合外力做的功(包括克服重力做功和克服摩擦阻力做功),
损失的动能为:△Ek=mgh+fh=(mg+f)h?①
损失的机械能等于克服摩擦阻力做功,△E=fh?②
由①②得:△Ek△E=mg+ff=常数,与h无关,由题意知此常数为3.
则物体上升到最高点时,动能为0,即动能减少了60J,那么损失的机械能为20J,
那么物体返回到底端,物体又要损失的机械能为20J,故物体从开始到返回原处总共机械能损失40J,因而它返回A点的动能为20J.
答:返回底端时动能应为20J.
本题解析:
本题难度:一般
2、选择题 关于“车沿斜坡匀速向坡顶运动”过程中涉及的相关物理问题,某研究性学习小组的同学在交流时有以下几种说法,其中错的是:(?)
A.此过程中合外力做正功;
B.此过程中汽车的重力做负功;
C.此过程中牵引力的功率不变;
D.此过程中汽车的重力势能增加。
参考答案:A
本题解析:由于车做的是匀速运动,动能不变,合外力做功为零,但重力做负功,选项A错误;故选B正确;由受力平衡分析可知牵引力不变,由P=Fv可知牵引力的功率不变,选项C正确;重力做负功重力势能增大,选项D正确;故选A
点评:本题难度较小,合外力做功根据动能变化判断,重力势能变化根据重力做功判断
本题难度:一般
3、选择题 如图所示,质量为M,半径为R的四分之一圆弧状木块,放在光滑的水平面,其中PQ段水平,P点是圆弧最低点。一个质量为m的小球从最高点开始自由滑下,不考虑一切摩擦,以下结论正确的是(?)
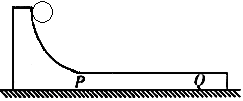
A.小球达到P点时,小球的速度为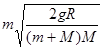
B.小球达到P点时,木块的速度为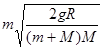
C.在到达P点瞬间小球对木块的压力大于mg
D.在到达P点瞬间小球对木块的压力等于mg
参考答案:BC
本题解析:
本题主要考查牛顿第二定律、动量守恒和机械能守恒定律的条件,需要注意的是滑块从最高点到P的过程中,系统动量不守恒,但在水平方向上动量守恒,因为系统在水平方向上没有受到外作作用。解题时还需注意到达P点瞬间小球有向心加速度,所受合外力不为零。
小球从最高点下滑到P的过程中,系统在水平方向上动量守恒、机械能守恒,令小球到达P点时的速度为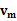 ,木块的的速度
,木块的的速度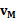 ,则:由水平方向动量守恒得
,则:由水平方向动量守恒得
mvm+MvM=0?(1)
由机械能守恒定律可得 ?(2)
?(2)
由方程(1)、(2)解得: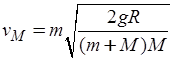
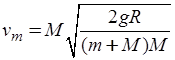
故A错误,B正确;小球到达P点瞬间具有向心加速度,所受合力不为零,由牛顿第二定律知小球受到的支持力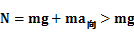 ?,由牛顿第三定律知小球对木块的压力
?,由牛顿第三定律知小球对木块的压力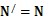 ,故C正确,D错误。
,故C正确,D错误。
所以选BC。
本题难度:简单
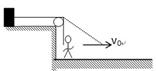
4、填空题 (4分)如图所示,质量为m的物体静止放在水平光滑的平台上,系在物体上的绳子跨过光滑定滑轮,在地面上的人以速度 向右匀速行走,设人从地面上靠近平台的边缘处开始向右行至绳与水平方向夹角θ=45°处,则在此过程中人对物体所做的功为?.
向右匀速行走,设人从地面上靠近平台的边缘处开始向右行至绳与水平方向夹角θ=45°处,则在此过程中人对物体所做的功为?.
参考答案: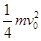
本题解析:人对物体所做的功等于物体增加的动能。
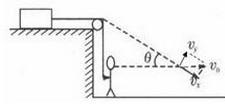
人以速度 向右行至绳与水平方向夹角θ=45°处时,物体的速度
向右行至绳与水平方向夹角θ=45°处时,物体的速度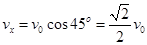 ,所以动能
,所以动能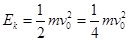
本题难度:一般
5、计算题 (12分)“∟”形轻杆两边互相垂直、长度均为l,可绕过O点的水平轴在竖直平面内自由转动。两端各固定一个金属小球A、B;其中A球质量为m、带负电、电荷量为q(q > 0);B球不带电,质量为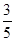 m。重力加速度为g 。现将“∟”形杆从OB位于水平位置由静止释放。已知sin37°=0.6,cos37°=0.8。求:
m。重力加速度为g 。现将“∟”形杆从OB位于水平位置由静止释放。已知sin37°=0.6,cos37°=0.8。求:
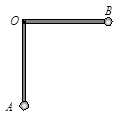
(1)A、B两球的最大动能之和为多少?
(2)若在空间加竖直向下的匀强电场,OB杆仍从原来位置释放后,能转过的最大角度为127°,则该电场的电场强度大小为多少?
参考答案:(1)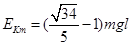 ?(2)
?(2)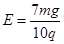
本题解析:(1)设转过θ角时系统的总动能为Ek。由机械能守恒定律得:
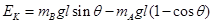 ? 2分
? 2分
整理得: ? 1分
? 1分
设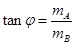 ,则:
,则:
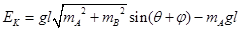 ?2分
?2分
由上式可知,当sin(θ +φ)= 1时,系统的总动能最大,设为Ekm,则:
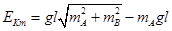 ? 1分
? 1分
由题意得:
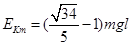 ? 2分
? 2分
(2)到达最大角度时,两球动能为零,由功能关系得:
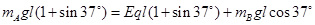 ? 2分
? 2分
解得: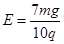 ? 2分
? 2分
本题难度:一般