1、单选题  某单位选举工会主席，每人投票从甲、乙、丙三个候选人中选择一人。已知该单位共有52人，并且在计票过程中的某时刻，甲得到17票，乙得到16票，丙得到11票。如果得票比其它两人都多的候选人将成为工会主席，那么甲最少再得到多少票就能够保证当选?_____
A: 2
B: 3
C: 4
D: 5
参考答案: C
本题解释:正确答案是C考点抽屉原理问题解析剩余的票数为：52-17-16-11=8，假设甲得4票，乙得4票，那甲仅以一票的优势当选，此时再少一票甲就不能保证当选，因此甲最少再得4张票就能保证当选，故正确答案为C。标签构造调整

2、单选题  甲某打电话时忘记了对方电话号码最后一位数字，但记得这个数字不是"0"。甲某尝试用其他数字代替最后一位数字，恰好第二次尝试成功的概率是_____。
A: 1/9
B: 1/8
C: 1/7
D: 2/9
参考答案: A
本题解释:正确答案是A考点概率问题解析最后一个数字不是0，共有9种选择。要求恰好第二次尝试成功，则第一次尝试失败，概率为8/9，第二次更换数字成功，概率为1/8，因此恰好第二次尝试成功的概率为8/9×1/8=1/9。故正确答案为A。秒杀技根据不放回摸球模型，恰好第二次尝试成功的概率与恰好第一次成功的概率相同，因此该概率值为1/9。故正确答案为A。

3、单选题  三位数的自然数N满足：除以6余3，除以5余3，除以4也余3，则符合条件的自然数N有几个?_____
A: 8
B: 9
C: 15
D: 16
参考答案: C
本题解释:正确答案是C考点余数与同余问题解析由题意可知满足同余情形，例如此题”三位自然数N除以6余3，除以5余3，除以4也余3”，可见余数恒为3，则取3，因此N的表达式为60n+3，其中60为6、5、4的最小公倍数，根据题目中的N为三位数，可得不等式100≤60n+3≤999，解得2≤n≤16，因此符合条件的自然数有15个，故正确答案为C选项。注：同余问题需要如下口诀：余同取余，和同加和，差同减差，最小公倍数做周期。口诀解释：余同取余，例如本题，余数恒为3，则取3;合同加和，例如”一个数除以7余1，除以6余2，除以5余3”，可见除数与余数的和相同，取此和8，被除数的表达式为210n+8;差同减差，例如”一个数除以7余3，除以6余2，除以5余1”。可见除数和余数的差相同，取此差4，被除数的表达式为210-4，其中210为5、6、7的最小公倍数。秒杀技根据题目，符合要求的数出现的周期为6、5、4的最小公倍数60，也即每60个连续自然数中必然有一个符合要求，三位数共有900个，因此符合要求的三位数共有900÷60=15(个)，故正确答案为C选项。标签最小公倍数同余问题

4、单选题  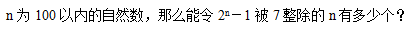_____ A: 32
B: 33
C: 34
D: 35
参考答案: B
本题解释:正确答案是B考点余数与同余问题解析

5、单选题  早上7点两组农民开始在麦田里收割麦子，其中甲组20人，乙组15人。8点半，甲组分出10个人捆麦子;10点，甲组将本组所有已割的麦子捆好后，全部帮乙组捆麦子;如果乙组农民一直在割麦子，什么时候乙组所有已割麦子能够捆好?(假设每个农民的工作效率相同)_____
A: 10：45
B: 11：00
C: 11：15
D: 11：30
参考答案: B
本题解释:正确答案是B考点工程问题解析采用赋值思想，设每个农民割麦子的效率为1，由题意可得，甲组割麦子的总量为20×1.5+10×1.5=45，故每个农民捆麦子的效率为45÷1.5÷10=3;设从10点之后经过n小时，乙组的麦子全部捆好。故乙组割麦子的总量为15×(3+n)，捆麦子总量为20×3×n，两值应相等，即45+15n=60n，解得n=1，即再过1小时就全部捆好了，此时为11：00。故正确答案为B。标签赋值思想