1、单选题  一直角三角形的两直角边的长度之和为14，假如这个三角形的周长与面积数值相等，那么该三角形的面积为_____。
A: 20
B: 22.5
C: 24
D: 24.5
参考答案: C
本题解释:正确答案是C考点几何问题解析

2、单选题  公路上有三辆同向行驶的汽车，其中甲车的时速为63公里，乙、丙两车的时速均为60公里，但由于水箱故障，丙车每连续行驶30分钟后必须停车2分钟。早上10点，三车到达同一位置，问1小时后，甲、丙两车最多相距多少公里?_____
A: 5
B: 7
C: 9
D: 11
参考答案: B
本题解释:正确答案是B考点行程问题解析在这1个小时中，丙车最多休息4分钟，也即丙在一个小时内最少行程为60×56÷60=56公里。而甲车持续行驶，可达63公里。因此两车最多相距7公里，故正确答案为B。

3、单选题  出租车队去机场接某会议的参与者，如果每车坐3名参与者，则需另外安排一辆大巴送走余下的50人，如每车坐4名参与者，则最后正好多出3辆空车。则该车队有多少辆出租车?_____[/content]
A: 50
B: 55
C: 60
D: 62
参考答案: D
本题解释:正确答案是D考点盈亏问题解析设共有n辆车。由题意可得，3n+50=4(n-3)，解得n=62。故正确答案为D。

4、单选题  某城市居民用水价格为：每户每月不超过5吨的部分按4元/吨收取;超过5吨不超过10吨的部分按6元/吨收取;超过10吨的部分按8元/吨收取。某户居民两个月共交水费108元，则该户居民这两个月用水总量最多为多少吨?_____
A: 17.25
B: 21
C: 21.33
D: 24
参考答案: B
本题解释:参考答案:B
题目详解:解法一：在花费相同的情况下，要使两个月用水量最多，须使水价相对较便宜阶段的用水量最大即两个月的“不超过5吨”和“5吨到10吨”部分的水量尽量多，通过计算2×(4×5+6×5)=100元，剩余180-100=8元，由于超出10吨的部分按8元/吨收取，故用水量为2×10+1=21吨，因此，选B。解法二：水量越大，费用越高，所以要用水最多，所以每个月应该用满10吨，所以总吨数为：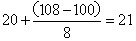

5、单选题  有一条公路长900米，在公路的一侧从头到尾每隔10米栽一根电线杆，可栽多少根电线杆?_____。
A: 82
B: 76
C: 91
D: 102
参考答案: C
本题解释:参考答案:C
题目详解:根据题意，公路全长可以分成若干段，由于公路的两端都要求栽杆，这是植树问题的变形，为两端均植树问题。确定总长：900确定间距：10带入两端均植树问题的公式：棵数=总长÷间距+1=900÷10+1=91所以，选C。考查点:数量关系>数学运算>特殊情境问题>植树问题>两端均植树