1、某公司要在长、宽、高分别为50米、40米、30米的长方体建筑的表面架设专用电路管道联接建筑物内最远两点，预设的最短管道长度介于_____。
A: 70—80米之间B: 60—70米之间C: 90—100米之间D: 80—90米之间
参考答案: D 本题解释:正确答案是D考点几何问题解析

2、某厂生产一批商标，形状为等边三角形或等腰三角形。已知这批商标边长为2cm或4cm，那么这批商标的周长可能是_____。
A: 6cm12cmB: 6cm8cm12cmC: 6cm10cm12cmD: 6cm8cm10cm12cm
参考答案: C 本题解释:正确答案是C考点几何问题解析三角形的两边之和必须大于第三边，因此三边可能有三种情况：(2，2，2)、(2，4，4)、(4，4，4)，周长为分别为6cm、10cm、12cm，故正确答案为C。

3、连接正方体每个面的中心构成一个正八面体(如下图所示)。已知正方体的边长为6厘米，则正八面体的体积为_____立方厘米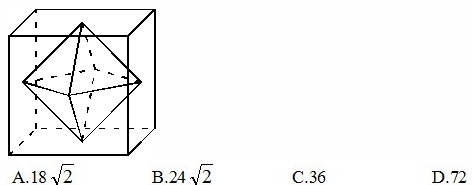
A: AB: BC: CD: D
参考答案: C 本题解释:正确答案是C考点几何问题解析秒杀技该正八面体可看成上下两个正四棱锥组成，注意到每个四棱锥的底面面积为正方体底面面积的一半，每个四棱锥的高为立方体棱长的一半，因此可知每个四棱锥的体积为正方体体积的1/12，故该正八面体体积为正方体体积的1/6，于是其体积为1/6×6^3=36。

4、用直线切割一个有限平面，后一条直线与此前每条直线都要产生新的交点，第1条直线将平面分成2块，第2条直线将平面分成4块。第3条直线将平面分成7块，按此规律将平面分为22块需_____。
A: 如果A、B、P不在同一条直线上，汽车所在位置有3个，可位于A、B两地之间或A、B两地外侧B: 如果A、B、P不在同一条直线上，汽车的位置有无穷多个C: 如果A、B、P位于同一条直线上，汽车拉于A、B两地之间或两地外侧D: 如果A、B、P位于同一条直线上，汽车位于A、B两地外侧，且汽车到A的距离为20千米
参考答案: D 本题解释:正确答案是B考点几何问题解析AB距离为40，AP和BP距离之和为60千米，若A、B、P三点在同一直线上，则P点位于AB外侧10千米处;若A、B、P三点不在同一直线上，则转化为A、B点固定，AP+BP=60即可，有无数种选择。故答案为B。

5、_____
A: AB: BC: CD: D
参考答案: D 本题解释:正确答案是D考点几何问题解析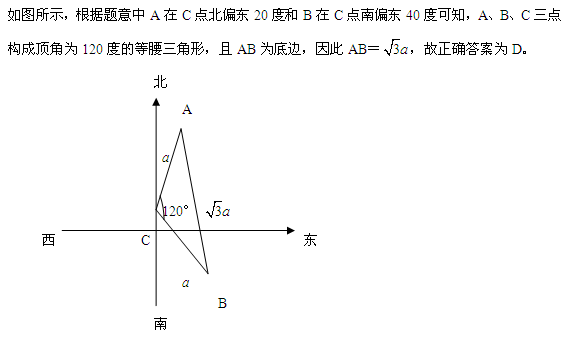标签画图分析

6、在下图中，大圆的半径是8。求阴影部分的面积是多少?_____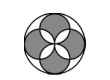
A: 120B: 128C: 136D: 144
参考答案: B 本题解释:正确答案是B考点几何问题解析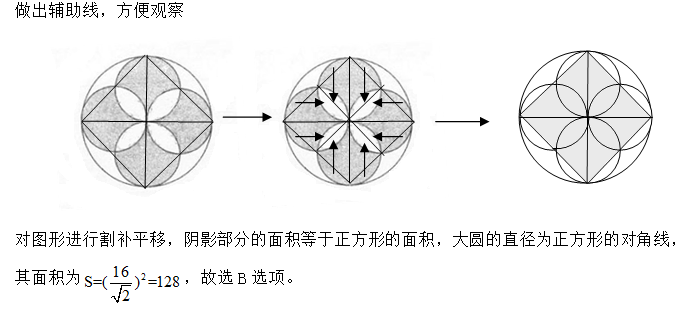

7、科考队员在冰面上钻孔获取样本，测量不同空心之间的距离，获得的部分数据分别为1米、3米、6米、12米、24米、48米。问科考队员至少钻了多少个孔?_____
A: 4B: 5C: 6D: 7
参考答案: D 本题解释:正确答案是D考点几何问题解析所测距离组成一个数列1、3、6、12、24、48，易知该数列中任一项均大于其前面所有项之和，故这6条线段不可能组成封闭回路，即6条线段最少7个端点，至少钻7个孔。故正确答案为D。

8、_____
A: AB: BC: CD: D
参考答案: B 本题解释:正确答案是B考点几何问题解析因为正三角形的周长和正六边形的周长相等，又因为正三角形和正六边形的边长的个数比是1：2，所以其边长之比为2：1，假设正三角形的边长为2，则正六边形的边长为1。正六边形可以分成6个小正三角形，如下图所示，边长为1的小正三角形面积：加长为2的正三角形面积=1：4。所以正六边形面积：正三角形面积=6：4=1.5，故正确答案为B。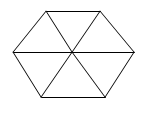标签赋值思想

9、相同表面积的四面体，六面体，正十二面体以及正二十面体，其中体积最大的是_____。
A: 四面体B: 六面体C: 正十二面体D: 正二十面体
参考答案: D 本题解释:正确答案是D考点几何问题解析根据等量最值原理，同样表面积的空间几何图形，越接近于球，体积越大。而四个选项中，正二十面体最接近于球，所以体积最大。故正确答案为D。

10、用一个平面将一个边长为1的正四面体切分为两个完全相同的部分，则切面的最大面积为_____。
A: AB: BC: CD: D
参考答案: B 本题解释:正确答案是B考点几何问题解析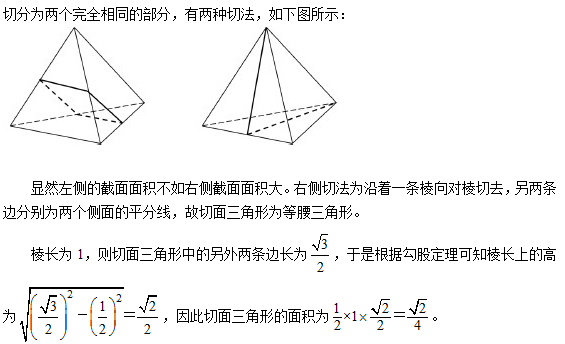故正确答案为B。标签勾股定理画图分析

11、一条路上依次有A、B、C三个站点，加油站M恰好位于A、C的中点，加油站N恰好位于B、C的中点，若想知道M和N两个加油站之间的距离，只需知道哪两点之间的距离?_____
A: B和CB: C和NC: A和MD: A和B
参考答案: D 本题解释:正确答案是D考点几何问题解析画图分析可知，MN=AC/2-BC/2=(AC-BC)/2=AB/2，则只需知道AB的距离，就可知道MN的距离。故正确答案为D。

12、长为1米的细绳上系有一个小球，从A处放手以后，小球第一次摆到最低点B处共移动了多少米?_____
A: 1+(1/3)πB: 1/2+(1/2)πC: (2/3)πD: 1+(2/3)π
参考答案: A 本题解释:正确答案是A考点几何问题解析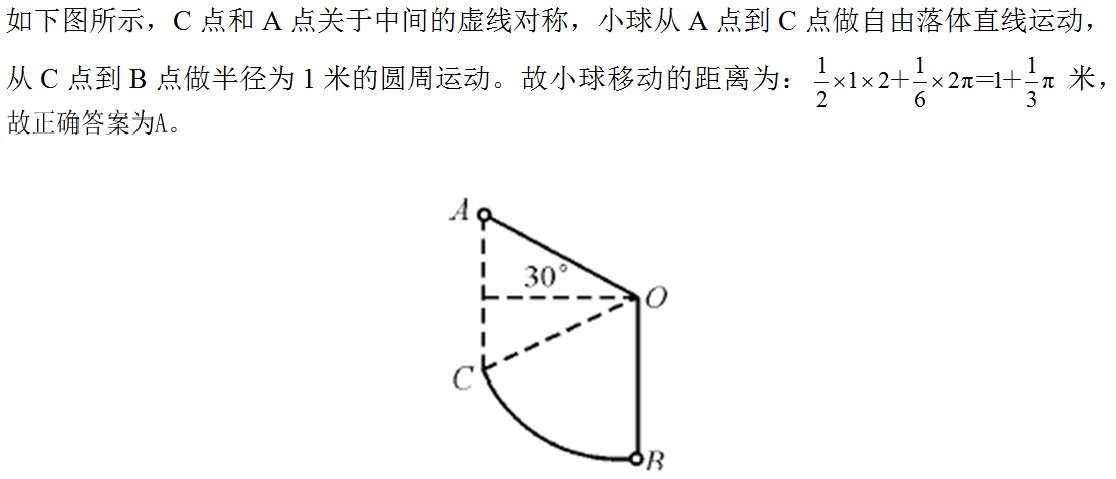备注：本题中所求长度的线条即有线段与圆弧两部分组成，正确把握分界点是解题关键。考题中的分界点一般与物理常识相关。

13、现有边长1米的一个木质正方体，已知将其放入水里，将有0.6米浸入水中。如果将其分割成边长0.25米的小正方体，并将所有的小正方体都放入水中，直接和水接触的表面积总量为_____。
A: 3.4平方米B: 9.6平方米C : 13.6平方米D: 16平方米
参考答案: C 本题解释:正确答案是C考点几何问题解析秒杀技对大正方体，易得其浸在水中的面积为3.4平方米，恰为选项A。而分解过小正方体后总浸水面积比为比值的倍数。故正确答案为C。

14、把一个正四面体的每个表面都分成9个相同的等边三角形，用任意颜色给这些小三角形上色，要求有公共边的小三角形颜色不同，问最多有多少个小三角形颜色相同?_____
A: 15B: 12C: 16D: 18
参考答案: A 本题解释:正确答案是A考点几何问题解析先看一个面上的情况，要是颜色相同的三角形最多，最多有6个(如下图左侧图所示)，此时其他面上能与之颜色相同的三角形最多只能有3个(如下图右侧图所示)。因此颜色相同的三角形最多有6+3×3=15个，正确答案为A。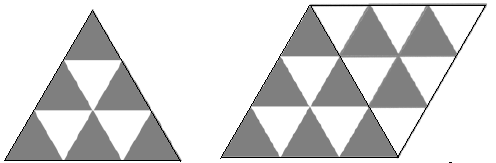标签画图分析

15、甲、乙两个容器均有50厘米深，底面积之比为5:4，甲容器水深9厘米，乙容器水深5厘米，再往两个容器各注入同样多的水，直到水深相等，这时两容器的水深是_____。
A: 20厘米B: 25厘米C: 30厘米D: 35厘米
参考答案: B 本题解释:正确答案是B考点几何问题解析设注入水后的水深为y厘米，则根据注入水同样多，可知(y-9)×5=(y-5)×4，解得y=25，故正确答案为B。

16、_____
A: AB: BC: CD: D
参考答案: A 本题解释:正确答案是A考点几何问题解析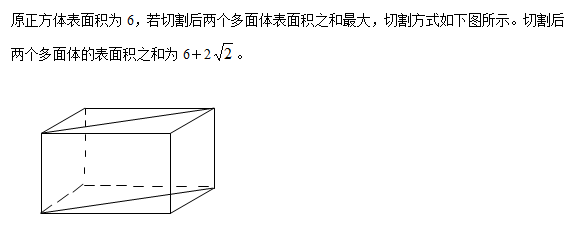

17、3颗气象卫星与地心距离相等，并可同时覆盖全球地表，现假设地球半径为R，则3颗卫星距地球最短距离为_____。
A: RB: 2RC: R/2D: 2R/3
参考答案: A 本题解释:正确答案是A考点几何问题解析故正确答案为A。

18、长方形ABCD的面积是72平方厘米，E、F分别是CD、BC的中点，三角形AEF的面积是多少平方厘米?_____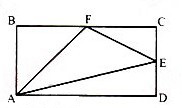
A: 24B: 27C: 36D: 40
参考答案: B 本题解释:正确答案是B考点几何问题解析三角形AEF虽然为规则几何图形，但不是特殊的三角形，且三边值未知，若正面求解较为麻烦。从逆向考虑，注意到△AEF可以看作长方形依次去除周围三个三角形得到。由比例关系可知，△ABF为长方形的1/4，△ADE为长方形的1/4，而△ECF为长方形的1/8，因此△AEF为长方形大小的3/8，故可知其面积为27，故正确答案为B。标签逆向考虑

19、气象台测得在S岛正东方向80千米处，一台风中心正以20千米/小时的速度沿北偏西60度的方向匀速移动。若台风中心50千米范围内为影响区域，台风中心移动方向不变、强度不变，该台风对S岛的影响时间约持续_____。
A: 2小时B: 3小时C: 4小时D: 5小时
参考答案: B 本题解释:正确答案是B考点几何问题解析故正确答案为B。