1、单选题  某大学某班学生总数为32人。在第一次考试中有26人及格，在第二次考试中有24人及格。若两次考试中都没有及格的有4人，那么两次考试都及格的人数是_____。
A: 22
B: 18
C: 28
D: 26
参考答案: A
本题解释:正确答案是A考点容斥原理问题解析由题意，两次考试中至少有一次及格的人数为32-4=28(人)，设两次考试都及格的人数是n，则有：28=26﹢24-n，解得n=22。故正确答案为A。注：两集合容斥原理公式为A∪B=A+B-A∩B。标签两集合容斥原理公式

2、单选题  三位数的自然数P满足：除以7余2，除以6余2，余以5也余2，则符合条件的自然数P有_____。
A: 2个
B: 3个
C: 4个
D: 5个
参考答案: C
本题解释:正确答案是C考点余数与同余问题解析解析1：由题可知，该数减去2应当同时为5、6、7的倍数，5、6、7的最小公倍数为210，故满足条件的三位数有210+2=212，210×2+2=422，210×3+2=632，210×4+2=842，共四个数字。故正确答案为C。解析2：根据口诀：余同取余，和同加和，差同减差，最小公倍数做周期。知道满足余同，该自然数P满足P=210n+2，又P是三位数，则100≤210n+2≤999，解得：1≤n≤4。满足条件的n有4个。故正确答案为C。标签最小公倍数

3、单选题  如下图：已知直线P
A:y=kx+4与直线P
B:y=x+b相交于P(1，2)，且分别与x轴、y轴交于点A、B。则四边形OAPB的面积是_____。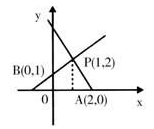A: A
B: B
C: C
D: D
参考答案: C
本题解释:正确答案是C解析已知P
A:y=kx+4与直线P
B:y=x+b相交于P(1，2)。则k+4=2，1+b=2，解得k=-2，b=1，故P
A:y=-2x+4，P
B:y=x+1。PB与x轴交点为(-1，0)，则底边长为2-(-1)=3。故有3×2÷2-1×1÷2=2.5，故正确答案为C。考点几何问题

4、单选题  某项射击资格赛后的表明，某国四名运动员中，三名运动员的平均环数加上另一运动员的环数，计算后得到的环数分别为92、114、138、160，则此国四名运动员资格赛的平均环数是_____。
A: 63
B: 126
C: 168
D: 252
参考答案: A
本题解释:正确答案是A考点平均数问题解析四名运动员的平均环数必然小于任意三名运动员环数加上另一名的环数。选项中只有A<92，符合条件。故正确答案为A。

5、单选题  某地劳动部门租用甲、乙两个教室开展农村实用人才培训。两教室均有5排座位，甲教室每排可坐10人，乙教室每排可坐9人。两教室当月共举办该培训27次，每次培训均座无虚席，当月培训1290人次。问甲教室当月共举办了多少次这项培训?_____
A: 8
B: 10
C: 12
D: 15
参考答案: D
本题解释:正确答案是D考点和差倍比问题解析乙教室可坐9人，可知乙培训过的人数含有因子3，而总的培训人数1290也含有因子3，因此甲教室培训过的人数也必然含有3因子。而甲教室可坐50人，因此要使甲教室培训过的人数也含有3因子，则其举办次数必然含有3因子，因此只有C、D符合。将C选项代入，可知此时乙教室举办过15次培训，其总人数的尾数为5，而甲教室培训的总人数尾数总是为0，因此甲、乙教室的培训人数尾数为5，不符合要求。故正确答案为D。秒杀技由题意，甲教室每次培训50人，乙教室每次培训45，假设甲乙的次数分别为X、Y，则可得50X+45Y=1290，观察等式可知45Y的尾数必然为0，因此Y必然为偶数，从而X为奇数，仅D符合。故正确答案为D。