|
微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
C.64 D.63
[答案]B
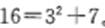 [解析]基于“数形敏感”,由数列的三、四、五项可以得出 。经过验证有: [解析]基于“数形敏感”,由数列的三、四、五项可以得出 。经过验证有:
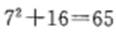 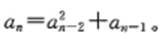 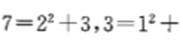 2,故该数列的通项为 因此,所填数字为 ,答案为B。 2,故该数列的通项为 因此,所填数字为 ,答案为B。

【真题精析】
例1、2,12,36,80,( )
A.100 B.125 C.150 D.175
[答案]C
[解析]基于“数字敏感”,数列的第四项80可以拆分成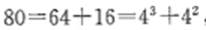 ,第三项可以拆分成36= ,第三项可以拆分成36=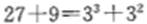 ,基于“数列敏感”,可以推测数列是由平方数列和立方数列相加得到,经过验证有2=1+1 ,基于“数列敏感”,可以推测数列是由平方数列和立方数列相加得到,经过验证有2=1+1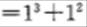 , ,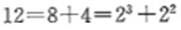 ,故数列的通项公式为 ,故数列的通项公式为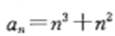 。因此,所求数字为 。因此,所求数字为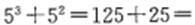 150,答案选C。 150,答案选C。

【真题精析】
例1、6,12,36,102,( ),3
A.24 B.71 C.38 D.175
[答案]A
[解析]数列各项都可以被3整除。
六、数字推理秒杀技巧

【真题精析】
例1. (2003·山东)2,10,30,68,130,( )
A.169 B.222 C.181 D.231
[答案]B
[秒杀技巧]数列各项均为偶数,观察选项,三奇一偶。因此,选B。
[解析]原数列各项减自身项数是立方数列。www.91exAm.ORG

【真题精析】
例1.(2007·福建)3,7,15,31,( )
A.23 B.62 C.63 D.64
[答案]C
[秒杀技巧]观察原数列,各项均为奇数,排除B、D。数列单调递增,排除A。因此,选C。
[解析]数列通项为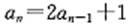 ,故所填数字为2×31+1=63。 ,故所填数字为2×31+1=63。

【真题精析】
例1. (2008·浙江)675,225,90,45,30,30,( )
A.27 B.38 C.60 D.124
[答案]C
[秒杀技巧]数列各项均能被15整除,分析选项,只有C符合。
[解析]相邻两项做商(前项除以后项)得到:3,2.5,2,1.5,1,(o.5),所填数字为60。

【真题精析】
例1、(2008·辽宁)15,5,3,5/3,( )

[答案]A
[秒杀技巧] 观察选项,分母5出现2次,故分母选为5;分子9出现2次,故分子选为9。因此,选A。
[解析] 原数列通项公式为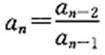
附件一:运算部分各种题型和思想的潜心研究
数学运算可以说是行测当中最费时费力的一种题型了,具有速度和难度测验的双重性质,这类题型测试的范围很广,涉及的知识点很多,但是2/3的部分都是基础部分,我们需要把这些基础部分的方法牢记,掌握主要的题型有路程问题、工程问题、尾数计算问题、比较大小问题等,其他类型的问题会在更新中不断增加,其关键还是要掌握方法,能熟练掌握方法就能在考场上大大节约时间。同时要掌握一些常用的数学技巧,尽量用简便方法,理解题意,掌握一定的题型和解题方法,加强训练,主要练速度。那么下面针对这几种题型在国考中的真题来讨论一下解题方法。
基础板块1、路程问题,这类问题分为相遇问题、追及问题、流水问题
相遇问题要把握的核心是“速度和”的问题,即A、B两者所走的路程和等于速度和*相遇时间;追及问题要把握的核心是“速度差”的问题,即A走的路程减去B走的路程等于速度差*追及时间;流水问题,为节省空间只需记住以下结论:船速=(顺水速度+逆水速度)除以2,水速=(顺水速度—逆水速度)除以2.当然题目不会单纯明显的考你相遇、追及、流水问题,存在许多变形。
(03中央)姐弟俩出游,弟弟先走一步,每分钟走40米,走了80米后姐姐去追他。姐姐每分钟走60米,姐姐带的小狗每分钟跑150米。小狗追上了弟弟又转去找姐姐,碰上了姐姐又转去追弟弟,这样跑来跑去,直到姐弟相遇小狗才停下来。问小狗共跑了多少米?
A.600米 B.800米
C.1 200米 D.1 600米
答案:A设x分钟后相遇,则40x+80=60x。则x=4。
因小狗的速度为150米/分钟,故小狗的行程为150×4=600,故A正确
2、工程问题,个人觉得这类题目还是比较简单的,可以把全工程看做1个单位,工作要N天完成其工作效率就是1/N,两人共同完成就是1/n1+1/n2,工程问题有许多变形,如水池灌水之类的,思路是一样的。
(07中央)一篇文章 ,现有甲乙丙三人,如果由甲乙两人合作翻译,需要 10 小时完成,如果由乙丙两人合作翻译,需要12 小时完成。现在先由甲丙两人合作翻译4 小时,剩下的再由乙单独去翻译,需要12 小时才能完成,则,这篇文章
如果全部由乙单独翻译,要( ) 小时能够完成.
A.15 B . 18 C . 20 D .25
答案:A各自设为 1/X,1/Y,1/Z,列出方程即可求解
3、尾数计算问题,对于此类问题要知道,和的尾数是一个加数的尾数加上另一个加数的尾数,差、积、商都有同样的道理
(05中央)173*173*173-162*162*162=()
A.926183 B.936185 C 926187 D 926189
答案:D 因为3*3*3-2*2*2=19,所以是D
4、比较大小问题,有三种方法作差、作商、找中间值,找中间值比较经典。比如4/9,3/7,151/301,拿它们分别与1/2比较就可以看出大小了。
5、过河问题,这种问题是比较恼人的题目,不过掌握了方法后还是知道如何应对的。先看题目
有a,b,c,d四人在晚上都要从桥的左边到右边。桥一次最多两人,只有一个手电,过桥必须手电。四人过桥速度a2分钟,b 3分钟,c 8分钟,d 10分钟,走得快的要等走得慢的,问所有人过最短要()分钟
A 22 B21 C20 D 19
答案:B这类题目要按这种顺序来1、过河最短次最短先过2、已过的最短时间的人返回3、过河最长时间的和次最长的过4、已过次最短的人返回5、剩下过河时间最短和次最短的人过河,重复以上过程直至走完
6、日期问题,这种问题主要就是看最后的余数。你比如
2003 年 7 月 1 日 是星期二,那么 2005 年 7 月 1 日是:
A 星期三 B 星期四 C 星期五 D 星期六
答案:C。2004 年是闰年,共有 366 天,所以从 2003 年 7 月 1 日 到 2005 年 7 月 1 日 共有 731 天。 731 除以 7 的余数等于 3 , 2003 年 7 月 1 日 是星期二,则 2005 年 7 月 1 日 是星期五。
7、缴费问题,这种问题有几种方法,常规方法速度慢,这里只讲速度最快的方法。如:
(08中央)为节约用水,某市决定用水收费实行超额超收,标准用水量以内每吨2.5元,超过标准的部分加倍收费。某用户某月用水15吨,交水费62.5元,若该用户下个月用水12吨,则应交水费多少钱?
A.42.5元 B.47.5元 C.50元 D.55元
答案:B如果该用户15吨水全部都交5元钱/吨,则他应当交75元水费,比实际缴纳额少了12.5元。少缴纳的12.5元是因为未超出标准用水量的部分每吨少缴纳2.5元。因此标准水量为12.5÷2.5=5吨,知道标准水量剩下的直接求就可以了。
8、鸡兔同笼的变式,这种题目的思想是假设,假设全是鸡,算出脚数,与题目中给出的脚数比较,看差多少,每差一个(4-2)只就说明有一只兔子,将所差脚数除以(4-2),就可以求出兔子数,同理假设全是兔,可以求出鸡数。
例:红铅笔每支0.19元,蓝铅笔每支0.11元,两种铅笔共买了16支,花了2.80元.问红、蓝铅笔各买几支?
解:以“分”作为钱的单位.我们设想,一种“鸡”有11只脚,一种“兔子”有19只脚,它们共有16个头,280只脚.现在已经把买铅笔问题,转化成“鸡兔同笼”问题了.
利用上面算兔数公式,就有:
蓝笔数=(19×16-280)÷(19-11)=24÷8=3(支).
红笔数=16-3=13(支).
答:买了13支红铅笔和3支蓝铅笔.
对于这类问题的计算,经常可以利用已知脚数的非凡性.例2中的“脚数”19与11之和是30.我们也可以设想16只中,8只是“兔子”,8只是“鸡”,根据这一设想,脚数是8×(11 19)=240.比280少40.40÷(19-11)=5。就知道设想中的8只“鸡”应少5只,也就是“鸡”(蓝铅笔)数是3.
30×8比19×16或11×16要轻易计算些.利用已知数的非凡性,靠心算来完成计算.实际上,可以任意设想一个方便的兔数或鸡数。
例如,设想16只中,“兔数”为10,“鸡数”为6,就有脚数
19×10 11×6=256,比280少24。
24÷(19-11)=3,
就知道设想6只“鸡”,要少3只。要使设想的数,能给计算带来方便,经常取决于你的心算本领。
9、牛吃草问题变式
牛吃草原题,天气变冷,牧场上草以每天均匀速度减少。经计算,牧场草可供20头牛吃5天,或者16头牛吃6天。那么可供11头牛吃几天?
这类问题的数量关系是(牛数*吃草较多天数-牛数*吃草较少天数)/(吃草较多天数-吃草较少天数)=草地每天新长草量
牛数*吃草天数-草地每天新长草量*吃草天数=原有草量,把握这两个式子这类问题就OK啦
例:有一个水池,池底有一出水口,5台抽水机20小时抽完,8台抽水机15小时抽完。仅靠出水口出水,要多长时间出完?
A 25小时 B 30小时 C 40小时 D 45小时
答案:D 每小时漏水(8*15-5*20)/(20-15)=4份水,原来有水8*15+4*15=180份,故180/4=45小时
10、时钟问题的所有解法,解时钟方面的问题一般是做两面钟的时差或者速度比,另外记住这几个结论也是相当的重要的,时针每小时走30度,分针每小时走360度,分针走一分钟(6度),时针走0.5度,两者速度差为5.5度。另外涉及钟表图形时候你可以画个草图,分针是要比时针长。
(05中央)一个快钟每小时比标准时间快 1 分钟,一个慢钟每小时比标准时间慢 3 分钟。如将两个钟同时调到标准时间,结果在 24 小时内,快钟显示 10 点整时,慢钟恰好显示 9 点整。则此时的标准时间是:
A 9 点 15 分 B 9 点 30 分 C 9 点 35 分 D 9 点 45 分
答案:D(快钟-标准):(标准-慢钟)=1:3,那么当快钟10点,慢钟9点,按1:3进行时间划分就可以得到标准时间是9点45了
从12点到13点,钟的时针和分针可成直角的机会有()
A 1次 B2次 C 3次 D 4次
[yc]答案:B理论上可以判断出2 |