|
微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
解】将方程组和方程合并,后可得线性方程组
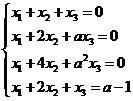
其系数矩阵
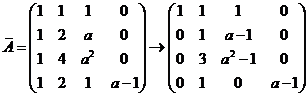 . .
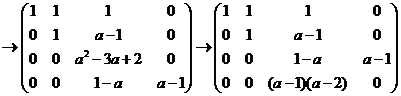 . .
显然,当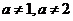 时无公共解. 时无公共解.
当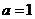 时,可求得公共解为 时,可求得公共解为 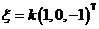 , ,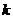 为任意常数; 为任意常数;
当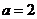 时,可求得公共解为 时,可求得公共解为 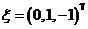 . .
【评注】本题为基础题型,考查非齐次线性方程组解的判定和结构.
(24) (本题满分11分)
设三阶对称矩阵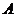 的特征向量值 的特征向量值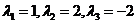 , ,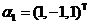 是 是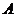 的属于 的属于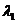 的一个特征向量,记 的一个特征向量,记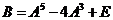 ,其中 ,其中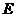 为3阶单位矩阵. 为3阶单位矩阵.
(I)验证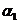 是矩阵 是矩阵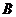 的特征向量,并求 的特征向量,并求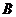 的全部特征值与特征向量; 的全部特征值与特征向量;
(II)求矩阵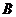 . .
【分析】本题考查实对称矩阵特征值和特征向量的概念和性质.
【详解】(I)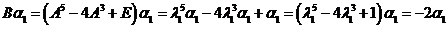 , ,
则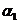 是矩阵 是矩阵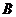 的属于-2的特征向量. 的属于-2的特征向量.
同理可得
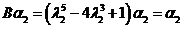 , ,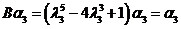 . .
所以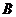 的全部特征值为2,1,1 的全部特征值为2,1,1
设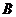 的属于1的特征向量为 的属于1的特征向量为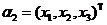 ,显然 ,显然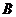 为对称矩阵,所以根据不同特征值所对应的特征向量正交,可得 为对称矩阵,所以根据不同特征值所对应的特征向量正交,可得
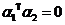 . .
即 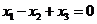 ,解方程组可得 ,解方程组可得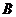 的属于1的特征向量 的属于1的特征向量
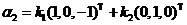 ,其中 ,其中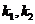 为不全为零的任意常数. 为不全为零的任意常数.
由前可知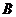 的属于-2的特征向量为 的属于-2的特征向量为 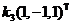 ,其中 ,其中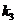 不为零. 不为零.
(II)令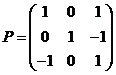 ,由(Ⅰ)可得 ,由(Ⅰ)可得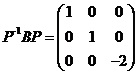 ,则 ,则
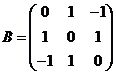 . .
【评注】本题主要考查求抽象矩阵的特征值和特征向量,此类问题一般用定义求解,要想方设法将题设条件转化为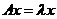 的形式. 请记住以下结论: 的形式. 请记住以下结论:
(1)设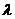 是方阵 是方阵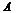 的特征值,则 的特征值,则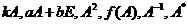 分别有特征值 分别有特征值
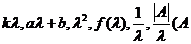 可逆),且对应的特征向量是相同的. 可逆),且对应的特征向量是相同的.
(2)对实对称矩阵来讲,不同特征值所对应的特征向量一定是正交的 |