微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
所以 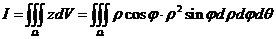
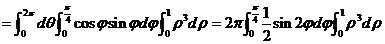
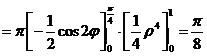 .
.
四、(本题满分6分.)
【解析】直接展开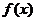 相对比较麻烦,可
相对比较麻烦,可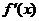 容易展开,
容易展开,
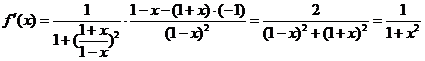 .
.
由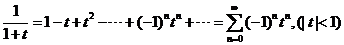 ,令
,令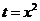 得
得
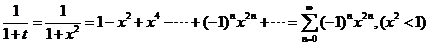
即 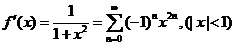
所以
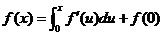 ,
,
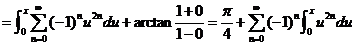
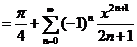
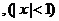
当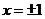 时,式
时,式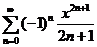 均收敛,而左端
均收敛,而左端 在
在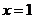 处无定义.
处无定义.
因此 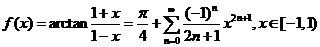 .
.
五、(本题满分7分.)
【解析】先将原式进行等价变换,再求导,试着发现其中的规律,
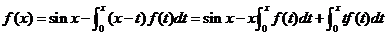 ,
,
所给方程是含有未知函数及其积分的方程,两边求导,得
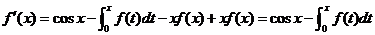 ,
,
再求导,得
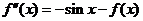 ,即
,即 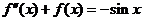 .
.
这是个简单的二阶常系数非齐次线性微分方程,对应的齐次方程的特征方程为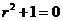 ,
,
此特征方程的根为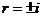 ,而右边的
,而右边的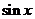 可看作
可看作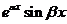 ,
,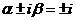 为特征根,因此非齐次方程有特解
为特征根,因此非齐次方程有特解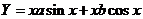 .
.
代入方程并比较系数,得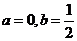 ,故
,故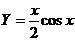 ,所以
,所以
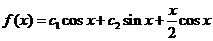 ,
,
又因为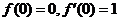 ,所以
,所以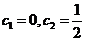 ,即
,即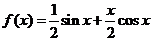 .
.
六、(本题满分7分.)
【解析】方法一:判定方程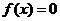 等价于判定函数
等价于判定函数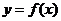 与
与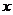 的交点个数.
的交点个数.
令 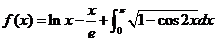 ,
,
其中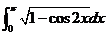 是定积分,为常数,且被积函数
是定积分,为常数,且被积函数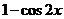 在
在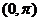 非负,故
非负,故
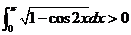 ,为简化计算,令
,为简化计算,令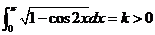 ,即
,即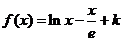 ,
,
则其导数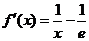 ,令
,令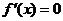 解得唯一驻点
解得唯一驻点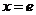 ,
,
即 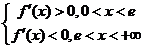 ,
,
所以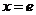 是最大点,最大值为
是最大点,最大值为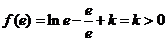 .
.
又因为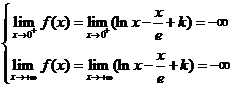 ,由连续函数的介值定理知在
,由连续函数的介值定理知在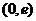 与
与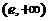 各有且仅有一个零点(不相同),故方程
各有且仅有一个零点(不相同),故方程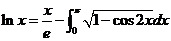 在
在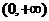 有且仅有两个不同实根.
有且仅有两个不同实根.
方法二: 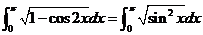 ,
,
因为当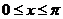 时,
时,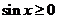 ,所以
,所以
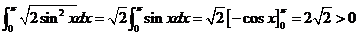 ,
,
其它同方法一.
七、(本题满分6分.)
【解析】对方程组的增广矩阵作初等行变换.
第一行分别乘以有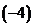 、
、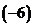 加到第二行和第三行上,再第二行乘以
加到第二行和第三行上,再第二行乘以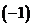 加到第三行上, 有
加到第三行上, 有
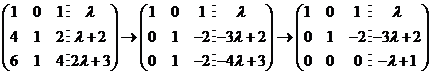 .
.
由于方程组有解的充要条件是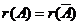 ,故仅当
,故仅当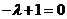 ,即
,即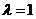 时,方程组有解.此时秩
时,方程组有解.此时秩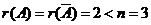 ,符合定理的第二种情况,故方程组有无穷多解.
,符合定理的第二种情况,故方程组有无穷多解.
由同解方程组 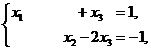 令
令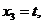 解得原方程组的通解
解得原方程组的通解
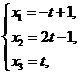 (其中
(其中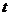 为任意常数).
为任意常数).
【相关知识点】1.非齐次线性方程组有解的判定定理:
设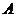 是
是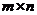 矩阵,线性方程组
矩阵,线性方程组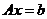 有解的充分必要条件是系数矩阵的秩等于增广矩阵
有解的充分必要条件是系数矩阵的秩等于增广矩阵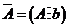 的秩,即是
的秩,即是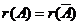 (或者说,
(或者说,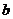 可由
可由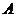 的列向量
的列向量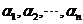 线表出,亦等同于
线表出,亦等同于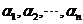 与
与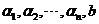 是等价向量组)
是等价向量组)
设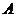 是
是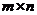 矩阵,线性方程组
矩阵,线性方程组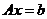 ,则
,则
(1) 有唯一解 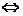
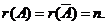
(2) 有无穷多解 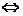
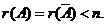
(3) 无解 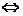
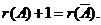
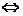
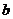 不能由
不能由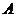 的列向量
的列向量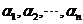 线表出.
线表出.
八、(本题满分8分.)
【解析】(1)由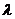 为
为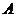 的特征值可知,存在非零向量
的特征值可知,存在非零向量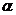 使
使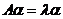 ,两端左乘
,两端左乘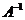 ,得
,得
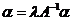 .因为
.因为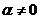 ,故
,故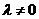 ,于是有
,于是有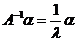 .按特征值定义知
.按特征值定义知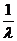 是
是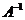 的特征
的特征
值.
(2)由于逆矩阵的定义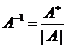 ,据第(1)问有
,据第(1)问有 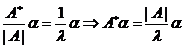 ,按特征值定义,即
,按特征值定义,即 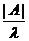 为伴随矩阵
为伴随矩阵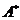 的特征值.
的特征值.
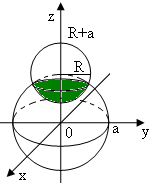 【相关知识点】矩阵特征值与特征向量的定义:设
【相关知识点】矩阵特征值与特征向量的定义:设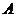 是
是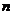 阶矩阵,若存在数
阶矩阵,若存在数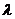 及非零的
及非零的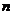 维列向量
维列向量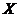 使得
使得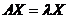 成立,则称
成立,则称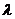 是矩阵
是矩阵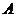 的特征值,称非零向量
的特征值,称非零向量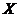 是矩阵
是矩阵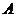 的特征向量.
的特征向量.
九、(本题满分9分.)
【解析】由球的对称性,不妨设球面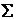 的球心是
的球心是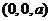 ,
,
于是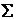 的方程是
的方程是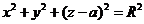 .
.
先求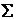 与球面
与球面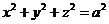 的交线
的交线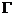 :
:
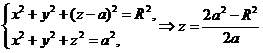 .
.
代入上式得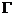 的方程
的方程 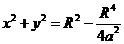 .
.
它在平面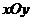 上的投影曲线
上的投影曲线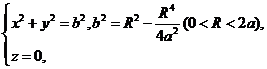
相应的在平面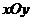 上围成区域设为
上围成区域设为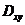 ,则球面
,则球面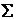 在定球面内部的那部分面积
在定球面内部的那部分面积
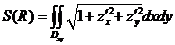 .
.
将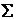 的方程两边分别对
的方程两边分别对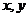 求偏导得
求偏导得
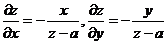 ,
,
所以 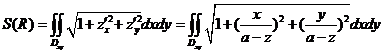
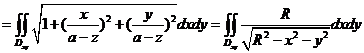 .
.
利用极坐标变换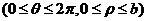 有
有
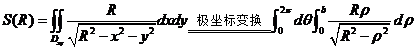
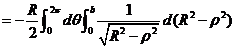
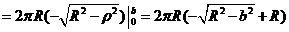
代入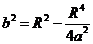 ,化简得
,化简得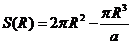 .
.
这是一个关于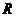 的函数,求
的函数,求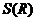 在
在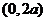 的最大值点,
的最大值点,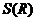 两边对
两边对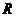 求导,并令
求导,并令
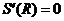 ,得
,得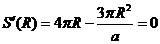 ,得
,得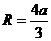 .
.
且 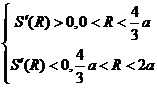 ,
,
故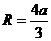 时
时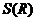 取极大值,也是最大值.
取极大值,也是最大值.
因此,当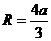 时球面
时球面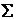 在定球面内部的那部分面积最大.
在定球面内部的那部分面积最大.
十、填空题(本题满分6分,每小题2分.)
(1)【解析】
方法一: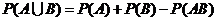
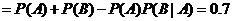 .
.
方法二: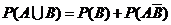
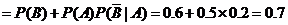 .
.
(2)【解析】设事件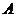 =“甲射中”,
=“甲射中”,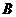 =“乙射中”,依题意,
=“乙射中”,依题意,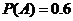 ,
,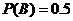 ,
,
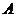 与
与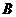 相互独立,
相互独立,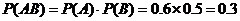 .
.
因此,有 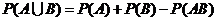
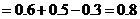 .
.
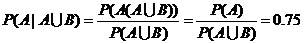 .
.
(3)【解析】设事件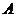 =“方程有实根”,而方程
=“方程有实根”,而方程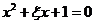 有实根的充要条件是其判别式
有实根的充要条件是其判别式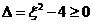 ,即
,即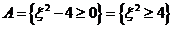 .
.
随机变量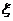 在(1,6)上服从均匀分布,所以其分布函数为
在(1,6)上服从均匀分布,所以其分布函数为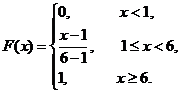
由分布函数的定义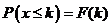 ,
,
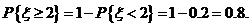 而
而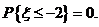
所以由概率的可加性,有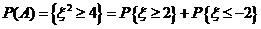
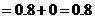 .
.
【相关知识点】广义加法公式: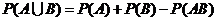 .
.
条件概率: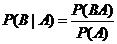 ,所以
,所以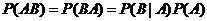 .
.
十一、(本题满分6分.)
【解析】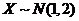 ,
,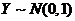 ,由独立的正态变量
,由独立的正态变量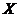 与
与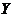 的线性组合仍服从正态分布,且
的线性组合仍服从正态分布,且
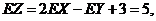
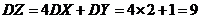 ,
,
得 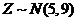 .
.
代入正态分布的概率密度公式,有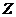 的概率密度函数为
的概率密度函数为 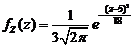 .
.
【相关知识点】对于随机变量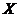 与
与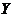 均服从正态分布,则
均服从正态分布,则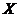 与
与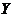 的线性组合亦服从正态分布.
的线性组合亦服从正态分布.
若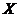 与
与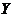 相互独立,由数学期望和方差的性质,有
相互独立,由数学期望和方差的性质,有
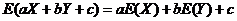 ,
,
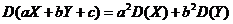 ,
,
其中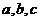 为常数.
为常数.