|
微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
限.

令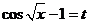 ,则 ,则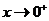 时 时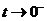 ,所以 ,所以
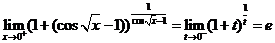 , ,
所以 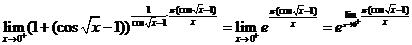 . .
因为当 时, 时, ,所以 ,所以
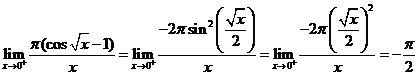 , ,
故 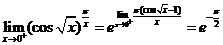 . .
(2)【解析】先求方向 的方向余弦,再求 的方向余弦,再求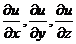 ,最后按方向导数的计算公式 ,最后按方向导数的计算公式
 求出方向导数. 求出方向导数.
曲面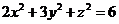 在点 在点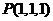 处的法向量为 处的法向量为
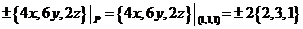 , ,
在点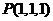 处指向外侧,取正号,并单位化得 处指向外侧,取正号,并单位化得

又 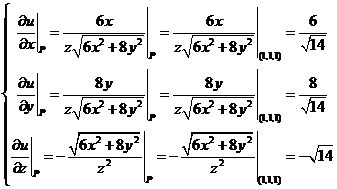 , ,
所以方向导数

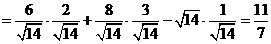 . .
(3)【解析】由曲线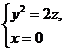 绕 绕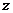 轴旋转一周而围成的旋转面方程是 轴旋转一周而围成的旋转面方程是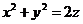 . .
 于是, 于是,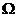 是由旋转抛物面 是由旋转抛物面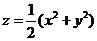 与平面 与平面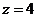 所围成.曲面与平面的交线是 所围成.曲面与平面的交线是
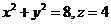 . .
选用柱坐标变换,令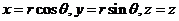 ,于是 ,于是
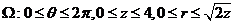 , ,
因此 


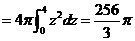 . .
四、(本题满分6分)
【解析】曲线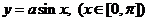 ,则 ,则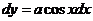 ,所以 ,所以






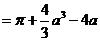 . .
对关于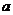 的函数 的函数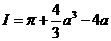 两边对 两边对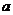 求导数,其中 求导数,其中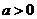 ,并令 ,并令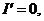 得 得
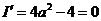 . .
所以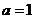 , 且 , 且 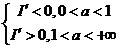 . .
故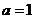 为函数 为函数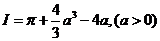 的极小值点,也是最小值点.故所求的曲线为 的极小值点,也是最小值点.故所求的曲线为
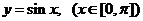 . .
五、(本题满分8分.)
【解析】按傅式级数公式,先求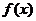 的傅式系数 的傅式系数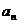 与 与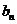 .因 .因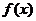 为偶函数,所以 为偶函数,所以
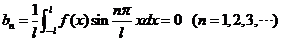 , ,


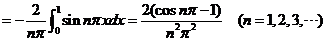 , ,
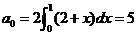 . .
因为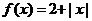 在区间 在区间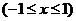 上满足狄利克雷收敛定理的条件,所以 上满足狄利克雷收敛定理的条件,所以


 . .
令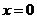 ,有 ,有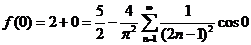 ,所以, ,所以,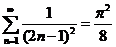 . .
又 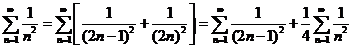 , ,
所以, 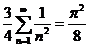 ,即 ,即 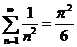 . .
六、(本题满分7分.)
【解析】由定积分中值定理可知,对于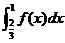 ,在区间 ,在区间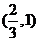 上存在一点 上存在一点 使得 使得
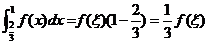 , ,
即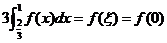 . .
由罗尔定理可知,在区间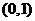 内存在一点 内存在一点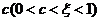 ,使得 ,使得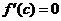 . .
七、(本题满分8分)
【解析】设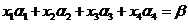 ,按分量写出,则有 ,按分量写出,则有
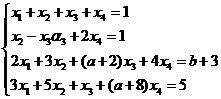 . .
对方程组的增广矩阵作初等行变换:
第一行分别乘以有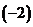 、 、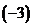 加到第三行和第四行上,再第二行乘以 加到第三行和第四行上,再第二行乘以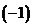 、 、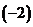 加到第三行和第四行上,有 加到第三行和第四行上,有

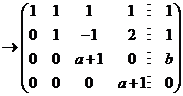 , ,
所以,当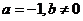 时, 时,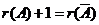 ,方程组无解.即是不存在 ,方程组无解.即是不存在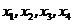 使得 使得
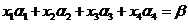 成立, 成立,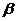 不能表示成 不能表示成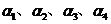 的线性组合; 的线性组合;
当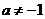 时, 时,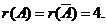 方程组有唯一解 方程组有唯一解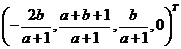 , ,
故 有唯一表达式,且 有唯一表达式,且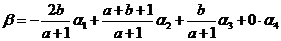 . .
【相关知识点】非齐次线性方程组有解的判定定理:
设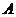 是 是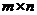 矩阵,线性方程组 矩阵,线性方程组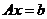 有解的充分必要条件是系数矩阵的秩等于增广矩阵 有解的充分必要条件是系数矩阵的秩等于增广矩阵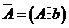 的秩,即是 的秩,即是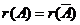 (或者说, (或者说,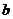 可由 可由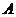 的列向量 的列向量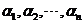 线表出,亦等同于 线表出,亦等同于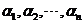 与 与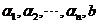 是等价向量组). 是等价向量组).
设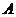 是 是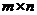 矩阵,线性方程组 矩阵,线性方程组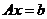 ,则 ,则
(1) 有唯一解 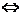 
(2) 有无穷多解 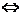 
(3) 无解 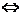 
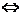 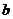 不能由 不能由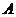 的列向量 的列向量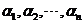 线表出. 线表出.
八、(本题满分6分)
【解析】方法1:因为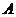 为 为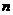 阶正定阵,故存在正交矩阵 阶正定阵,故存在正交矩阵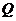 ,使 ,使
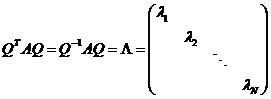 , ,
其中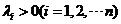 , ,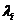 是 是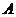 的特征值. 的特征值.
因此 
两端取行列式得 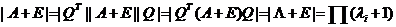 , ,
从而 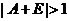 . .
方法2:设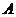 的 的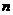 个特征值是 个特征值是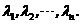 由于 由于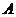 为 为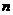 阶正定阵,故特征值全大于0. 阶正定阵,故特征值全大于0.
由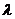 为 为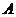 的特征值可知,存在非零向量 的特征值可知,存在非零向量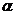 使 使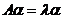 ,两端同时加上 ,两端同时加上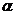 , ,
得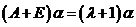 .按特征值定义知 .按特征值定义知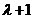 是 是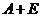 的特征值.因为 的特征值.因为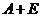 的特征值是 的特征值是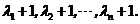 它们全大于1,根据 它们全大于1,根据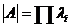 ,知 ,知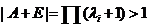 . .
【相关知识点】阵特征值与特征向量的定义:设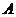 是 是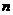 阶矩阵,若存在数 阶矩阵,若存在数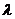 及非零的 及非零的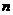 维列向量 维列向量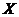 使得 使得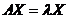 成立,则称 成立,则称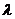 是矩阵 是矩阵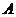 的特征值,称非零向量 的特征值,称非零向量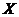 是矩阵 是矩阵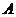 的特征向量. 的特征向量.
九、(本题满分8分)
【解析】曲线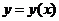 在点 在点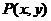 处的法线方程为 处的法线方程为
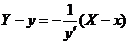 (当 (当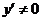 时), 时),
它与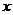 轴的交点是 轴的交点是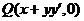 ,从而 ,从而
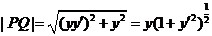 . .
当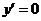 时,有 时,有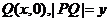 ,上式仍然成立. ,上式仍然成立.
因此,根据题意得微分方程
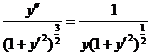 , ,
即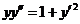 .这是可降阶的高阶微分方程,且当 .这是可降阶的高阶微分方程,且当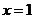 时, 时,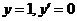 . .
令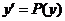 ,则 ,则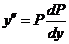 ,二阶方程降为一阶方程 ,二阶方程降为一阶方程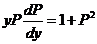 ,即 ,即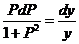 . .
即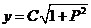 , ,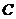 为常数. 为常数.
因为当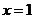 时, 时,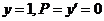 ,所以 ,所以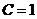 ,即 ,即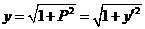 , ,
所以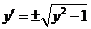 .分离变量得 .分离变量得 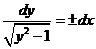 . .
令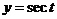 ,并积分,则上式左端变为 ,并积分,则上式左端变为

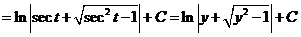 . .
因曲线在上半平面,所以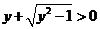 ,即 ,即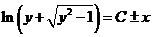 . .
故 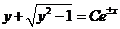 . .
当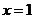 时, 时,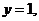
当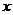 前取+时, 前取+时,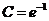 , ,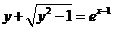 , ,
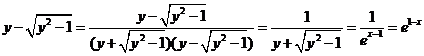 ; ;
当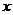 前取 前取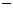 时, 时,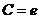 , ,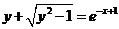 , ,
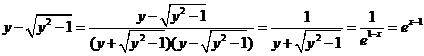 ; ;
所以 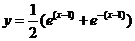 . .
十、填空题(本题满分6分,每小题3分.)
(1)【解析】一般说来,若计算正态分布随机变量在某一范围内取值的概率,应该已知分布的两个参数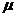 和 和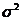 ,否则应先根据题设条件求出 ,否则应先根据题设条件求出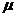 , ,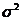 ,再计算有关事件的概率,本题可从 ,再计算有关事件的概率,本题可从
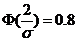 ,通过查 ,通过查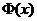 表求出 表求出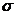 ,但是注意到所求概率 ,但是注意到所求概率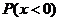 即是 即是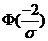 与 与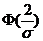 之间的关系,可以直接由 之间的关系,可以直接由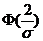 的值计算出 的值计算出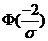 . .
因为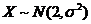 ,所以可标准化得 ,所以可标准化得 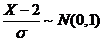 , ,
由标准正态分布函数概率的计算公式,有
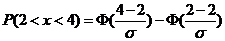 , ,
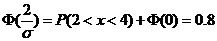 . .
由正态分布函数的对称性可得到 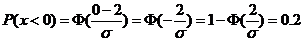 . .
(2)【解析】设事件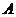 =“掷的点和原点的连线与 =“掷的点和原点的连线与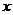 轴的夹角小于 轴的夹角小于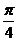 ”, ”,
 这是一个几何型概率的计算问题.由几何概率公式 这是一个几何型概率的计算问题.由几何概率公式
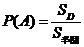 ,而 ,而 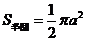 , ,
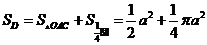 , ,
故 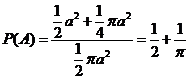 . .
十一、(本题满分6分)
【解析】二维连续型随机变量的概率等于对应区域的二重积分,所以有
 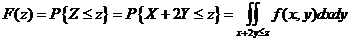 . .
当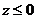 时, 时,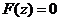 . .
因为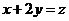 在直线 在直线 的下方 的下方
与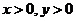 (即第一象限)没有公共区域, (即第一象限)没有公共区域,
所以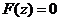 . .
当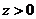 时, 时,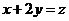 在直线 在直线
的上方与第一象限相交成一个三角形区域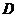 ,此即为积分区间. ,此即为积分区间.
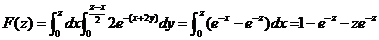 . .
所以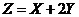 的分布函数 的分布函数 
|