微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
相关知识点】1.全概率公式:  ;
;
2. 古典型概率公式: .
.
二、选择题(本题共5小题,每小题3分,满分15分.每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内)
(1)【答案】(C)
【解析】这是讨论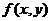 在
在 点是否连续,是否存在偏导数的问题.按定义
点是否连续,是否存在偏导数的问题.按定义
 ,
,
由于 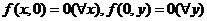 ,
,
 偏导数且
偏导数且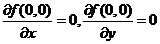 .
.
再看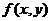 在
在 是否连续?由于
是否连续?由于
 ,
,
因此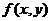 在
在 不连续.应选(C).
不连续.应选(C).
评注:① 证明分段函数在某点连续,一般要用定义证,有难度.证明分段函数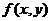 在某点
在某点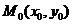 不连续的方法之一是:证明点
不连续的方法之一是:证明点 沿某曲线趋于
沿某曲线趋于 时,
时,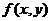 的极限不存在或不为
的极限不存在或不为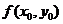 .
.
② 证明 不存在的重要方法是证明点
不存在的重要方法是证明点 沿两条不同曲线趋于
沿两条不同曲线趋于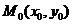 时,
时,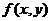 的极限不想等或沿某条曲线趋于
的极限不想等或沿某条曲线趋于 时,
时,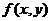 的极限不存在.
的极限不存在.
对于该题中的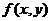 ,若再考察
,若再考察
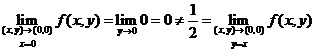 ,
,
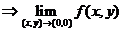 不存在.
不存在.
由本例可见,函数在一点处不连续,但偏导数却可以存在.容易找到这种例子,例如
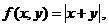 它在点
它在点 处连续,但
处连续,但 与
与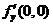 都不存在.可见二元函数的连续性与偏导数的存在性可以毫无因果关系.
都不存在.可见二元函数的连续性与偏导数的存在性可以毫无因果关系.
(2)【答案】(B)
 【解析】方法1:用几何意义.由
【解析】方法1:用几何意义.由 可知,曲线
可知,曲线 是上半平面的一段下降的凹弧,
是上半平面的一段下降的凹弧, 的图形大致如右图.
的图形大致如右图.
 是曲边梯形
是曲边梯形 的面积;
的面积;
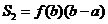 是矩形
是矩形 的面积;
的面积;
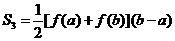 是梯形
是梯形 的面积.
的面积.
由图可见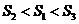 ,应选(B).
,应选(B).
方法2:观察法.因为是要选择对任何满足条件的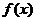 都成立的结果,故可以取满足条件的特定的
都成立的结果,故可以取满足条件的特定的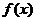 来观察结果是什么.例如取
来观察结果是什么.例如取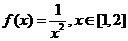 ,则
,则
 .
.
【评注】本题也可用分析方法证明如下:
由积分中值定理,至少存在一个点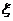 ,使
,使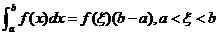 成立,再由
成立,再由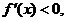 所以
所以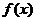 是单调递减的,故
是单调递减的,故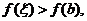 从而
从而
 .
.
为证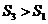 ,令
,令 则
则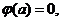
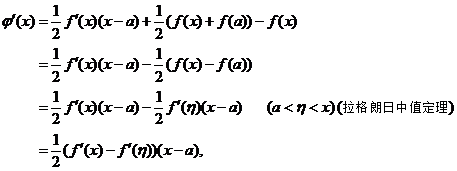
由于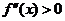 ,所以
,所以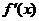 是单调递增的,故
是单调递增的,故 ,
, ,即
,即 在
在 上单调递增的.由于
上单调递增的.由于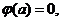 所以
所以 ,从而
,从而
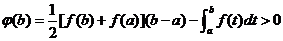 ,
,
即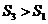 .因此,
.因此,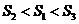 ,应选(D).
,应选(D).
如果题目改为证明题,则应该用评注所讲的办法去证,而不能用图证.
【相关知识点】1.积分中值定理:如果函数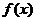 在积分区间
在积分区间 上连续,则在
上连续,则在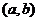 上至少存在一个点
上至少存在一个点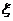 ,使下式成立:
,使下式成立: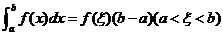 .这个公式叫做积分中值公式.
.这个公式叫做积分中值公式.
2. 拉格朗日中值定理:如果函数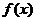 满足在闭区间
满足在闭区间 上连续,在开区间
上连续,在开区间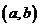 内可导,那么在
内可导,那么在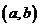 内至少有一点
内至少有一点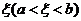 ,使等式
,使等式 成立.
成立.
(3)【答案】(A)
【解析】由于函数 是以
是以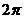 为周期的函数,所以,
为周期的函数,所以,
 ,
,
 的值与
的值与 无关.不选D,(周期函数在一个周期的积分与起点无关).
无关.不选D,(周期函数在一个周期的积分与起点无关).
估计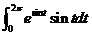 的值有多种方法.
的值有多种方法.
方法1:划分 取值正、负的区间.
取值正、负的区间.
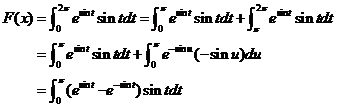
当 时,
时, ,
, 所以
所以 .选(A).
.选(A).
方法2:用分部积分法.

故应选(A).
【评注】本题的方法1十分有代表性.
被积函数在积分区间上可以取到正值与负值时,则常将积分区间划分成若干个,使每一个区间内,被积函数保持确定的符号,然后再作适当的变量变换,使几个积分的积分上下限相同,然后只要估计被积函数的正、负即可.
(4)【答案】(D)
【解析】方法1:三条直线交于一点的充要条件是方程组
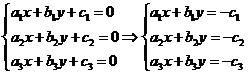
有唯一解.
将上述方程组写成矩阵形式: ,其中
,其中 是其系数矩阵,
是其系数矩阵, .则
.则 有唯一解
有唯一解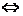
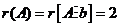 (方程组系数矩阵的秩与增广矩阵的秩相等且等于未知量的个数),即A的列向量组
(方程组系数矩阵的秩与增广矩阵的秩相等且等于未知量的个数),即A的列向量组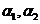 线性相关.所以应选(D).
线性相关.所以应选(D).
方法2:用排除法.
(A)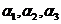 线性相关,当
线性相关,当 时,方程组的系数矩阵与增广矩阵的秩相等且小于未知量的个数,则①式有无穷多解,根据解的个数与直线的位置关系.所以三条直线重合,相交有无穷多点,(A)不成立.
时,方程组的系数矩阵与增广矩阵的秩相等且小于未知量的个数,则①式有无穷多解,根据解的个数与直线的位置关系.所以三条直线重合,相交有无穷多点,(A)不成立.
(B)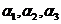 线性无关,
线性无关, 不能由
不能由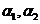 线性表出,方程组的系数矩阵与增广矩阵的秩不相等,方程组无解,根据解得个数与直线的位置关系,所以一个交点也没有,(B)不成立.
线性表出,方程组的系数矩阵与增广矩阵的秩不相等,方程组无解,根据解得个数与直线的位置关系,所以一个交点也没有,(B)不成立.
(C)秩 秩
秩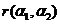 ,当
,当
 时,三条直线重合,不只交于一点,与题设条件矛盾,故(C)不成立.
时,三条直线重合,不只交于一点,与题设条件矛盾,故(C)不成立.
由排除法知选(D).
评注:应重视线性代数中的几何背景.空间直线方程及平面方程其在空间的位置关系应与线性代数中的线性相关性、秩及方程组的解及其充要条件有机的结合起来.
(5)【答案】(D)
【解析】因 与
与 独立,故
独立,故 和
和 也相互独立.由方差的性质,有
也相互独立.由方差的性质,有
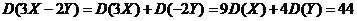 .
.
【相关知识点】方差的性质: 与
与 相互独立时,
相互独立时,
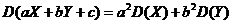 ,其中
,其中 为常数.
为常数.
三、(本题共3小题,每小题5分,满分15分.)
(1)【分析】三重积分的计算有三种方法:直角坐标中的计算,柱面坐标中的计算,球面坐标中的计算,其中柱面坐标中又可分先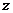 后
后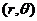 ,或先
,或先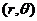 后
后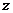 两种方法.本题的区域
两种方法.本题的区域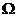 为绕
为绕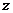 轴旋转的旋转体,用柱面坐标先
轴旋转的旋转体,用柱面坐标先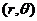 后
后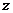 方便.
方便.
【解析】方法1:采用柱面坐标,先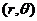 后
后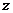 ,为此,作平面
,为此,作平面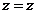 .
.
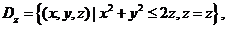
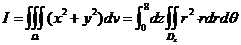 (将直角坐标化为柱面坐标)
(将直角坐标化为柱面坐标)
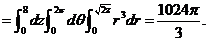
方法2:将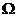 投影到
投影到 平面,得圆域
平面,得圆域 用柱面坐标先
用柱面坐标先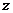 后
后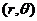 ,有
,有
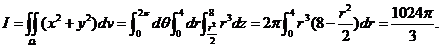
评注:做二次积分或三次积分时,如果里层积分的结果不含外层积分变量,那么里、外层积分可以分别积分然后相乘即可.如本例方法2中 可以单独先做.
可以单独先做.
(2)【解析】方法1:写出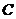 的参数方程,然后用曲线积分化为定积分的公式.
的参数方程,然后用曲线积分化为定积分的公式.
由平面上圆的参数方程易写出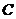 的参数方程为:
的参数方程为:
 ,
,
其中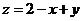 .
.
由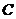 的方向知,
的方向知,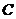 在
在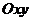 平面上的投影曲线相应地也是顺时针的,于是
平面上的投影曲线相应地也是顺时针的,于是 从
从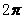 到0.
到0.
在把参数方程代入被积表达式之前,先用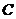 的方程将被积表达式化简,有
的方程将被积表达式化简,有
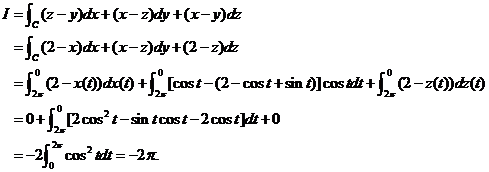
方法2:用斯托克斯公式来计算.记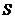 为平面
为平面 上
上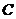 所围有限部分,由
所围有限部分,由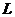 的定向,按右手法则
的定向,按右手法则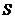 取下侧.
取下侧.
原积分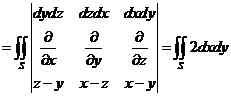 .
.
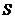 在
在 平面上的投影区域
平面上的投影区域 为
为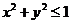 .将第二类曲面积分化为二重积分得
.将第二类曲面积分化为二重积分得
原积分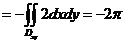 .
.
这里因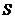 取下侧,故公式取负号.
取下侧,故公式取负号.
(3)【解析】已掌握新技术人数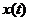 的变化率,即
的变化率,即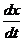 ,由题意可立即建立初值问题
,由题意可立即建立初值问题
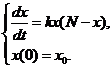
把方程分离变量得 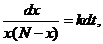
 .
.
积分可得 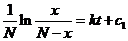 ,
, .
.
以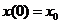 代入确定
代入确定 ,故所求函数为
,故所求函数为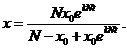
四、(本题共2小题,第(1)小题6分,第(2)小题7分,满分13分.)
(1)【分析】求出曲面 在点
在点 (位于
(位于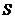 上)处的切平面方程,再写出
上)处的切平面方程,再写出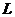 的参数方程,
的参数方程,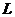 上的点的坐标应满足切平面方程,由此定出参数
上的点的坐标应满足切平面方程,由此定出参数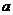 与
与 .
.
【解析】曲面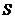 在点
在点 的法向量
的法向量
 .
.
切平面 的方程是
的方程是
 ,
,
即  .
.
将直线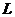 的方程改写成参数方程
的方程改写成参数方程
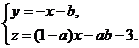
将它代入平面 方程得
方程得
 ,即
,即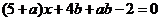 .
.
解得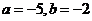 .
.
(2)【分析】 是由一元函数
是由一元函数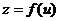 与二元函数
与二元函数 复合而成的二元函数,它满足方程
复合而成的二元函数,它满足方程
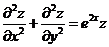 . (*)
. (*)
为了求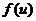 ,我们将用复合函数求导法,导出
,我们将用复合函数求导法,导出 ,
, ,
, ,
, 与
与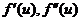 的关系,然后由(*)式导出
的关系,然后由(*)式导出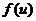 满足的常微分方程,从而求出
满足的常微分方程,从而求出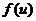 .
.
【解析】先用复合函数求导法导出
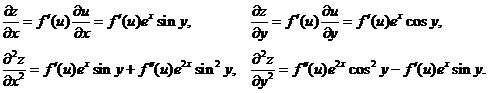
将后两式代入(*)得  ,即
,即 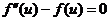 .
.
这是二阶线性常系数齐次方程,相应的特征方程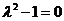 的特征根为
的特征根为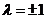 ,因此求得
,因此求得
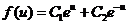 ,其中
,其中 、
、 为任意常数.
为任意常数.
五、(本题满分6分)
【分析】通过变换将 化为积分上限函数的形式,此时
化为积分上限函数的形式,此时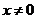 ,但根据
,但根据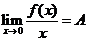 ,知
,知  ,从而
,从而 ,由此,利用积分上限函数的求导法则、导数在一点处的定义以及函数连续的定义来判定
,由此,利用积分上限函数的求导法则、导数在一点处的定义以及函数连续的定义来判定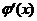 在
在 处的连续性.
处的连续性.
【解析】由题设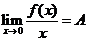 知,
知, 且有
且有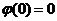 .又
.又
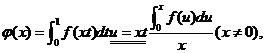
于是 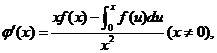
由导数定义,有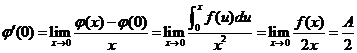 .
.
而 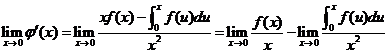
 ,
,
从而知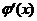 在
在 处连续.
处连续.
评注:对 作积分变量变换
作积分变量变换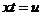 时,必附加条件
时,必附加条件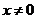 .因此,由
.因此,由 得到的
得到的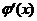 也附加有条件
也附加有条件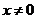 .从而
.从而 应单独去求.
应单独去求.
六、(本题满分8分)
【解析】(1)先证 单调有界.
单调有界.
显然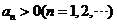 ,由初等不等式:对
,由初等不等式:对 非负数
非负数 必有
必有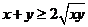 ,易知
,易知
 .
.
再考察 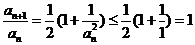 .
.
因此, 单调下降且有界,存在极限
单调下降且有界,存在极限 .
.
(2)方法1:由 单调下降
单调下降 .
.
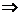 原级数是正项级数.现适当放大,注意
原级数是正项级数.现适当放大,注意 ,得
,得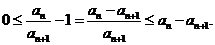
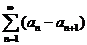 的部分和
的部分和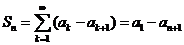 ,
,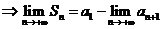 存在,可见级数
存在,可见级数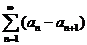 收敛.由比较判别法知,级数
收敛.由比较判别法知,级数 也收敛.
也收敛.
方法2:令 ,利用递推公式,有
,利用递推公式,有
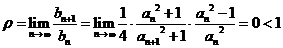 ,
,
由比值判别法知级数 也收敛.
也收敛.
【评注】由证明中可见,有下述结论: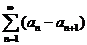 收敛
收敛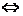
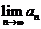 存在.
存在.
在考研题中多次用到这个知识点,考生可倍加注意.
七、(本题共2小题,第(1)小题5分,第(2)小题6分,满分11分.)
【分析】要求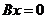 的解空间的一个标准基,首先必须确定此解空间的维数以及相应个数的线性无关的解.
的解空间的一个标准基,首先必须确定此解空间的维数以及相应个数的线性无关的解.
【解析】(1)因秩 ,故解空间的维数
,故解空间的维数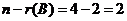 ,又因
,又因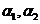 线性无关,
线性无关,
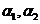 是方程组
是方程组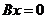 的解,由解空间的基的定义,
的解,由解空间的基的定义,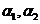 是解空间的基.
是解空间的基.
用施密特正交化方法先将其正交化,令:
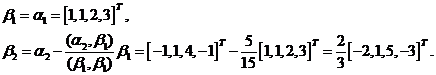
将其单位化,有  ,
,
即为所求的一个标准正交基.
评注:此题是一个基本计算题,只要求得一个齐次方程组的基础解系再标准正交化即可.
由于解空间的基不唯一,施密特正交化处理后标准正交基也不唯一.已知条件中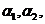
 是线性相关的(注意
是线性相关的(注意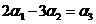 ),不要误认为解空间是3维的.
),不要误认为解空间是3维的.
(2)(I)设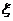 是矩阵
是矩阵 的属于特征值
的属于特征值 的特征向量,即
的特征向量,即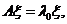
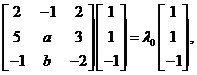
即 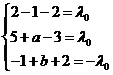
 .
.
(II)将(1)解得的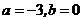 代入矩阵
代入矩阵 ,得
,得 .
.
其特征方程为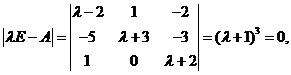
知矩阵 的特征值为
的特征值为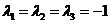 .
.
由于  ,
,
从而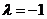 只有一个线性无关的特征向量,故
只有一个线性无关的特征向量,故 不能相似对角化.
不能相似对角化.
评注: 相似于对角阵
相似于对角阵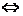 A的每个
A的每个 重特征值有
重特征值有 个线性无关的特征向量.
个线性无关的特征向量.
八、(本题满分5分)
【解析】由于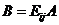 ,其中
,其中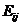 是初等矩阵
是初等矩阵

(1)因为 可逆,
可逆, ,故
,故 ,所以
,所以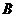 可逆.
可逆.
(2)由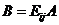 ,知
,知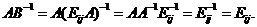
评注:①本题考查初等矩阵的概念与性质,要知道初等变换与初等矩阵左右乘的关系以及初等矩阵的逆矩阵的三个公式.有的考生写不出初等矩阵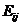 ,或将
,或将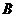 写成
写成 ,或不知道
,或不知道
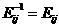 ,或认为
,或认为 ,而不知道
,而不知道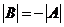 等,这些要引起注意.
等,这些要引起注意.
②经初等变换矩阵的秩不变,易知 ,也可证明
,也可证明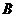 可逆.
可逆.
九、(本题满分7分)
【分析】首先需要清楚二项分布的产生背景.它的背景是:做 次独立重复试验,每次试验的结果只有两个(要么成功,要么失败),每次试验成功的概率都为
次独立重复试验,每次试验的结果只有两个(要么成功,要么失败),每次试验成功的概率都为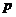 ,随机变量
,随机变量 表示
表示 次试验成功的次数,则
次试验成功的次数,则 .这道题中经过三个交通岗,在各个交通岗遇到红灯的事件是独立的,概率都为
.这道题中经过三个交通岗,在各个交通岗遇到红灯的事件是独立的,概率都为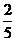 ,相当于做了3次独立重复试验,试验的结果只有两个(要么遇到红灯(成功),要么不遇到(失败)),每次成功的概率都为
,相当于做了3次独立重复试验,试验的结果只有两个(要么遇到红灯(成功),要么不遇到(失败)),每次成功的概率都为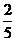 ,
, 表示遇到红灯的次数,相当于做了3次试验成功的次数,故
表示遇到红灯的次数,相当于做了3次试验成功的次数,故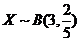 .
.
【解析】由题意知: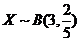 ,由二项分布的分布律的定义,有
,由二项分布的分布律的定义,有
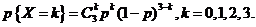
再由离散型随机变量分布函数的定义,有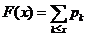 ,
,
(1)当 时,
时, ;
;
(2)当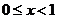 ,
, ;
;
(3)当 ,
,
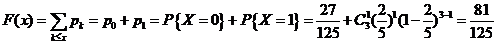 ;
;
(4)当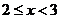 ,
,

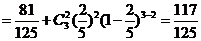 ;
;
(5)当 时
时
 .
.
因此 的分布函数为:
的分布函数为:
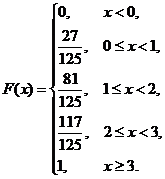
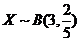 的数学期望为
的数学期望为 .
.
【相关知识点】1.二项分布分布律的定义: .
.
2.离散型随机变量分布函数的定义: .
.
3.二项分布 的期望为
的期望为 .
.
十、(本题满分5分)
【分析】矩估计的实质在于用样本矩来估计相应的总体矩,此题中被估参数只有一个,故只需要用样本一阶原点矩(样本均值)来估计总体的一阶原点矩(期望);最大似然估计,实质上就是找出使似然函数最大的那个参数,问题的关键在于构造似然函数.
【解析】(1)矩估计
由期望的定义: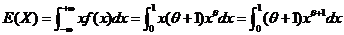
&nb