微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
1997考研数学一真题及答案详解
一、填空题(本题共5分,每小题3分,满分15分.把答案在题中横线上.)
(1) 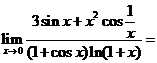 .
.
(2) 设幂级数 的收敛半径为3,则幂级数
的收敛半径为3,则幂级数 的收敛区间为 .
的收敛区间为 .
(3) 对数螺线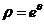 在点
在点 处的切线的直角坐标方程为 .
处的切线的直角坐标方程为 .
(4) 设 ,
,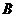 为三阶非零矩阵,且
为三阶非零矩阵,且 ,则
,则 = .
= .
(5) 袋中有50个乒乓球,其中20个是黄球,30个是白球,今有两人依次随机地从袋中各取一球,取后不放回,则第二个人取得黄球的概率是 .
二、选择题(本题共5小题,每小题3分,满分15分.每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内)
(1) 二元函数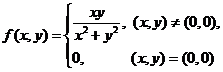 在点
在点 处 ( )
处 ( )
(A) 连续,偏导数存在 (B) 连续,偏导数不存在
(C) 不连续,偏导数存在 (D) 不连续,偏导数不存在
(2) 设在区间 上
上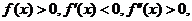 令
令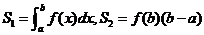 ,
,
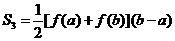 ,则 ( )
,则 ( )
(A) 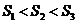 (B)
(B) 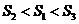
(C) 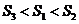 (D)
(D) 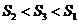
(3) 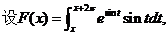 则
则 ( )
( )
(A) 为正常数 (B) 为负常数 (C) 恒为零 (D) 不为常数
(4) 设 则三条直线
则三条直线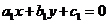 ,
,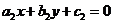 ,
,
 (其中
(其中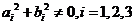 )交于一点的充要条件是 ( )
)交于一点的充要条件是 ( )
(A) 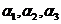 线性相关
线性相关
(B) 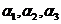 线性无关
线性无关
(C) 秩 秩
秩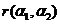
(D) 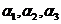 线性相关,
线性相关,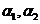 线性无关
线性无关
(5) 设两个相互独立的随机变量 和
和 的方差分别为4和2,则随机变量
的方差分别为4和2,则随机变量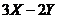 的方差是
的方差是
( )
(A) 8 (B) 16 (C) 28 (D) 44
三、(本题共3小题,每小题5分,满分15分.)
(1) 计算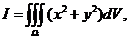 其中
其中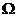 为平面曲线
为平面曲线 绕
绕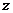 轴旋转一周形成的曲面与平面
轴旋转一周形成的曲面与平面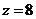 所围成的区域.
所围成的区域.
(2) 计算曲线积分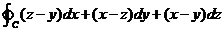 ,其中
,其中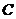 是曲线
是曲线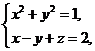 从
从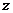 轴正向往
轴正向往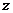 轴负向看,
轴负向看,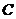 的方向是顺时针的.
的方向是顺时针的.
(3) 在某一人群中推广新技术是通过其中已掌握新技术的人进行的.设该人群的总人数为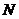 ,在
,在 时刻已掌握新技术的人数为
时刻已掌握新技术的人数为 ,在任意时刻
,在任意时刻 已掌握新技术的人数为
已掌握新技术的人数为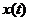 (将
(将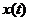 视为连续可微变量),其变化率与已掌握新技术人数和未掌握新技术人数之积成正比,比例常数
视为连续可微变量),其变化率与已掌握新技术人数和未掌握新技术人数之积成正比,比例常数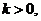 求
求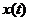 .
.
四、(本题共2小题,第(1)小题6分,第(2)小题7分,满分13分.)
(1) 设直线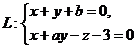 在平面
在平面 上,且平面
上,且平面 与曲面
与曲面 相切于点
相切于点 ,求
,求 之值.
之值.
(2) 设函数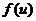 具有二阶连续导数,而
具有二阶连续导数,而 满足方程
满足方程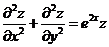 ,求
,求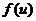 .
.
五、(本题满分6分)
设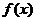 连续,
连续, 且
且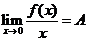 (
( 为常数),求
为常数),求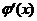 并讨论
并讨论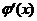 在
在 处的连续性.
处的连续性.
六、(本题满分8分)
设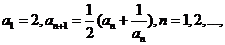 证明:
证明:
(1) 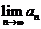 存在;
存在;
(2) 级数 收敛.
收敛.
七、(本题共2小题,第(1)小题5分,第(2)小题6分,满分11分.)
(1) 设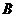 是秩为2的
是秩为2的 矩阵,
矩阵, 是齐次线性方程组
是齐次线性方程组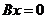 的解向量,求
的解向量,求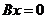 的解空间的一个标准正交基.
的解空间的一个标准正交基.
(2) 已知 是矩阵
是矩阵 的一个特征向量.
的一个特征向量.
(Ⅰ) 试确定参数 及特征向量
及特征向量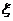 所对应的特征值;
所对应的特征值;
(Ⅱ) 问 能否相似于对角阵?说明理由.
能否相似于对角阵?说明理由.
八、(本题满分5分)
设 是
是 阶可逆方阵,将
阶可逆方阵,将 的第
的第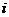 行和第
行和第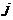 行对换后得到的矩阵记为
行对换后得到的矩阵记为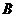 .
.
(1) 证明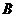 可逆;
可逆;
(2) 求 .
.
九、(本题满分7分)
从学校乘汽车到火车站的途中有3个交通岗,假设在各个交通岗遇到红灯的事件是相互独立的,并且概率都是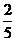 .设
.设 为途中遇到红灯的次数,求随机变量
为途中遇到红灯的次数,求随机变量 的分布律、分布函数和数学期望.
的分布律、分布函数和数学期望.
十、(本题满分5分)
设总体 的概率密度为
的概率密度为
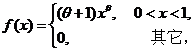
其中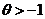 是未知参数.
是未知参数.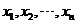 是来自总体
是来自总体 的一个容量为
的一个容量为 的简单随机样本,分别用矩估计法和最大似然估计法求
的简单随机样本,分别用矩估计法和最大似然估计法求 的估计量.
的估计量.
1997年全国硕士研究生入学统一考试数学一试题解析
一、填空题(本题共5分,每小题3分,满分15分.把答案在题中横线上.)
(1)【答案】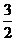
【分析】这是 型极限.注意两个特殊极限
型极限.注意两个特殊极限 .
.
【解析】将原式的分子、分母同除以 ,得
,得
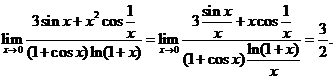
评注:使用洛必达法则的条件中有一项是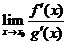 应存在或为
应存在或为 ,而本题中,
,而本题中,
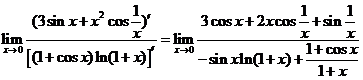
极限不存在,也不为 ,不满足使用洛必达法则的条件,故本题不能用洛必达法则.
,不满足使用洛必达法则的条件,故本题不能用洛必达法则.
【相关知识点】1.有界量乘以无穷小量为无穷小量.
(2)【答案】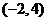
【解析】考察这两个幂级数的关系.令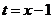 ,则
,则
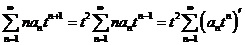 .
.
由于逐项求导后的幂级数与原幂级数有相同的收敛半径,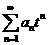 的收敛半径为3
的收敛半径为3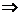
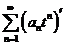 的收敛半径为3.从而
的收敛半径为3.从而 的收敛半径为3,收敛区间即(-3,3),回到原幂级数
的收敛半径为3,收敛区间即(-3,3),回到原幂级数 ,它的收敛区间为
,它的收敛区间为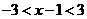 ,即
,即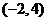 .
.
评注:幂级数的收敛区间指的是开区间,不考虑端点.
对于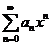 ,若
,若 它的收敛半径是
它的收敛半径是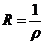 .但是若只知它的收敛半径为
.但是若只知它的收敛半径为 ,则
,则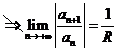 ,因为
,因为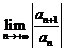 可以不存在(对于缺项幂级数就是这种情形).
可以不存在(对于缺项幂级数就是这种情形).
(3)【答案】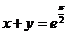
【解析】求切线方程的主要问题是求其斜率 ,而
,而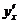 可由
可由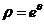 的参数方程
的参数方程
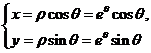
求得:  ,
,
所以切线的方程为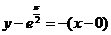 ,即
,即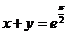 .
.
评注:本题难点在于考生不熟悉极坐标方程与直角坐标方程之间的关系.
(4)【答案】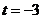
【解析】由 ,对
,对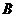 按列分块,设
按列分块,设 ,则
,则
 ,
,
即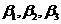 是齐次方程组
是齐次方程组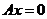 的解.
的解.
又因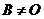 ,故
,故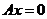 有非零解,那么
有非零解,那么
 ,
,
由此可得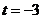 .
.
评注:若熟悉公式 ,则
,则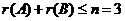 ,可知
,可知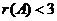 ,亦可求出
,亦可求出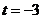 .
.
(5)【答案】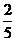
【解析】方法1:利用全概率公式.
求第二人取得黄球的概率,一般理解为这事件与第一人取得的是什么球有关.这就要用全概率公式.全概率公式首先需要一个完全事件组,这就涉及到设事件的问题.
设事件 “第
“第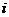 个人取得黄球”,
个人取得黄球”, ,则完全事件组为
,则完全事件组为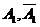 (分别表示第一个人取得黄球和第一个人取得白球).根据题设条件可知
(分别表示第一个人取得黄球和第一个人取得白球).根据题设条件可知
 ;
; ;
;
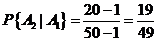 (第一个人取得黄球的条件下,黄球个数变成
(第一个人取得黄球的条件下,黄球个数变成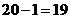 ,球的总数变成
,球的总数变成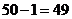 ,第二个人取得黄球的概率就为
,第二个人取得黄球的概率就为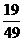 );
);
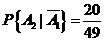 (第一个人取得白球的条件下,黄球个数亦为20,球的总数变成50-1=49,第二个人取得黄球的概率就为
(第一个人取得白球的条件下,黄球个数亦为20,球的总数变成50-1=49,第二个人取得黄球的概率就为 ).
).
故应用全概率公式
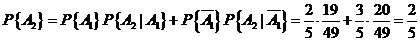 .
.
方法二:利用“抽签原理”.
只考虑第二个人取得的球,这50个球中每一个都会等可能地被第二个人取到.犹如几个人抽奖,其中只有一张彩票有奖,那么这几个人先抽与后抽,抽到有奖彩票的概率是一样的,这就是我们抽奖的公平性,此题中取到黄球的可能有20个,所以第二个人取到黄球的概率为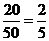 .
.
【