|
微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
特征值不同,故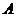 与 与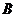 不相似,但它们的正惯性指数均为2,负惯性指数均为0.所以 不相似,但它们的正惯性指数均为2,负惯性指数均为0.所以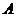 与 与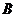 合同. 合同.
(5)【分析】 解本题的关键是明确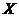 和 和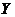 的关系: 的关系: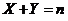 ,即 ,即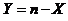 ,在此基础上利用性质:相关系数 ,在此基础上利用性质:相关系数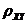 的绝对值等于1的充要条件是随机变量 的绝对值等于1的充要条件是随机变量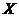 与 与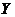 之间存在线性关系,即 之间存在线性关系,即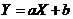 (其中 (其中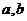 是常数),且当 是常数),且当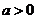 时, 时,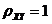 ;当 ;当 时, 时,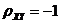 ,由此便知 ,由此便知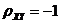 ,应选(A). ,应选(A).
事实上,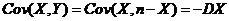 , ,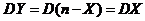 ,由此由相关系数的定义式有 ,由此由相关系数的定义式有 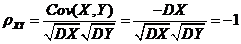 . .
三、【解】 原式=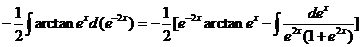
=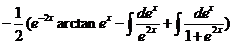
= . .
四、【解】 先求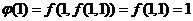 . .
求 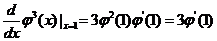 ,归结为求 ,归结为求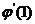 .由复合函数求导法 .由复合函数求导法
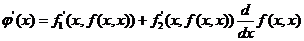 , ,
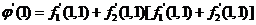 . .
注意 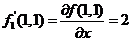 , ,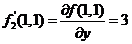 . .
因此 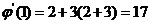 , ,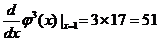 . .
五、【分析与求解】 关键是将 展成幂级数,然后约去因子 展成幂级数,然后约去因子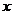 ,再乘上 ,再乘上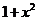 并化简即可. 并化简即可.
直接将 展开办不到,但 展开办不到,但 易展开,即 易展开,即
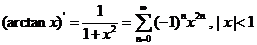 , ① , ①
积分得 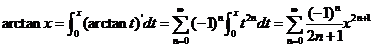 , ,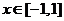 . ② . ②
因为右端积分在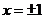 时均收敛,又 时均收敛,又 在 在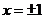 连续,所以展开式在收敛区间端点 连续,所以展开式在收敛区间端点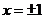 成立. 成立.
现将②式两边同乘以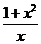 得 得
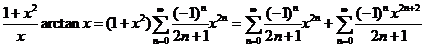
=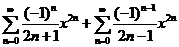
=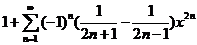
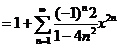 , , 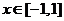 , ,
上式右端当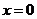 时取值为1,于是 时取值为1,于是
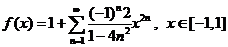 . .
上式中令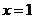 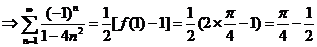 . .
六、【解】 用斯托克斯公式来计算.记 为平面 为平面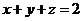 上 上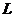 所 所
 为围部分.由 为围部分.由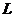 的定向,按右手法则 的定向,按右手法则 取上侧, 取上侧, 的单位法向量 的单位法向量
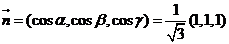 . .
于是由斯托克斯公式得
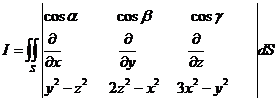
=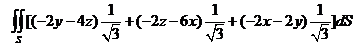
=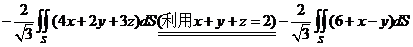 . .
于是 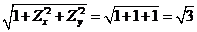 . .
按第一类曲面积分化为二重积分得
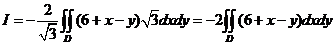 , ,
其中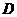 围 围 在 在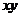 平面上的投影区域 平面上的投影区域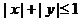 (图).由 (图).由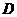 关于 关于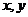 轴的对称性及被积函数的奇偶性得 轴的对称性及被积函数的奇偶性得 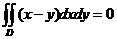
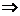 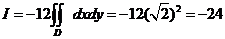 . .
七、【证明】 (1)由拉格朗日中值定理,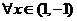 , ,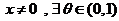 ,使 ,使
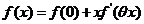
(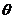 与 与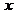 有关);又由 有关);又由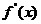 连续而 连续而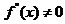 , ,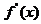 在 在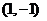 不变号, 不变号,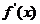 在 在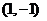 严格单调, 严格单调,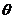 唯一. 唯一.
(2)对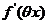 使用 使用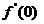 的定义.由题(1)中的式子先解出 的定义.由题(1)中的式子先解出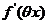 ,则有 ,则有
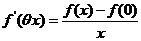 . .
再改写成 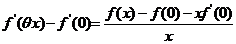 . .
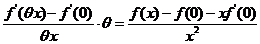 , ,
解出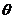 ,令 ,令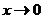 取极限得 取极限得
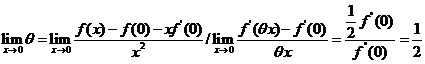 . .
八、【解】 (1)设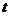 时刻雪堆的体积为 时刻雪堆的体积为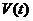 ,侧面积为 ,侧面积为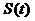 . .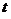 时刻雪堆形状如图所示 时刻雪堆形状如图所示
先求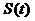 与 与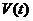 . .
侧面方程是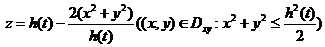 . .
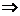 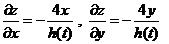 . .
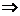 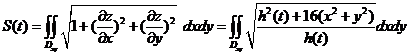 . .
作极坐标变换: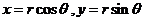 ,则 ,则
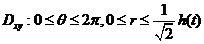 . .
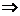 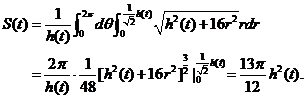
用先二后一的积分顺序求三重积分 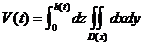 , ,
其中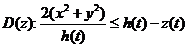 ,即 ,即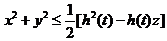 . .
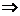 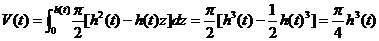 . .
(2)按题意列出微分方程与初始条件.
体积减少的速度是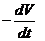 ,它与侧面积成正比(比例系数0.9),即 ,它与侧面积成正比(比例系数0.9),即 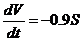
将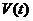 与 与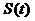 的表达式代入得 的表达式代入得 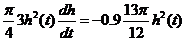 ,即 ,即
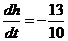 . ① . ①
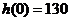 . ② . ②
(3)解①得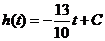 . 由②得 . 由②得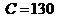 ,即 ,即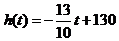 . .
令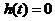 ,得 ,得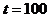 .因此,高度为130厘米的雪堆全部融化所需时间为100小时. .因此,高度为130厘米的雪堆全部融化所需时间为100小时.
九、【解】 由于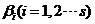 是 是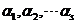 线性组合,又 线性组合,又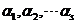 是 是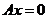 的解,所以根据齐次线性方程组解的性质知 的解,所以根据齐次线性方程组解的性质知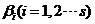 均为 均为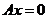 的解. 的解.
从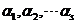 是 是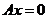 的基础解系,知 的基础解系,知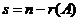 . .
下面来分析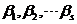 线性无关的条件.设 线性无关的条件.设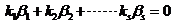 ,即 ,即
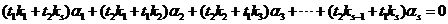 . .
由于 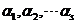 线性无关,因此有 线性无关,因此有
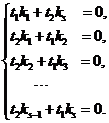
|