微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
2002考研数学一真题及答案详解
一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上)
(1)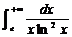 = _____________.
= _____________.
(2)已知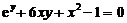 ,则
,则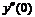 =_____________.
=_____________.
(3)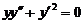 满足初始条件
满足初始条件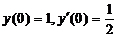 的特解是_____________.
的特解是_____________.
(4)已知实二次型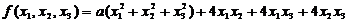 经正交变换可化为标准型
经正交变换可化为标准型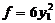 ,则
,则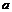 =_____________.
=_____________.
(5)设随机变量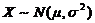 ,且二次方程
,且二次方程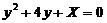 无实根的概率为0.5,则
无实根的概率为0.5,则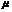 =_____________.
=_____________.
二、选择题(本题共5小题,每小题3分,满分15分.每小题给出的四个选项中,只有一个符合题目要求,把所选项前的字母填在题后的括号内)
(1)考虑二元函数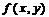 的四条性质:
的四条性质:
①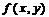 在点
在点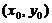 处连续, ②
处连续, ②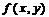 在点
在点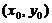 处的一阶偏导数连续,
处的一阶偏导数连续,
③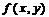 在点
在点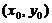 处可微, ④
处可微, ④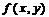 在点
在点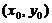 处的一阶偏导数存在.
处的一阶偏导数存在.
则有:
(A)②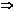 ③
③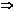 ① (B)③
① (B)③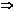 ②
②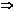 ①
①
(C)③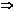 ④
④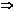 ① (D)③
① (D)③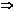 ①
①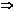 ④
④
(2)设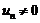 ,且
,且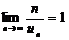 ,则级数
,则级数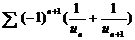 为
为
(A)发散 (B)绝对收敛
(C)条件收敛 (D)收敛性不能判定.
(3)设函数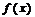 在
在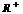 上有界且可导,则
上有界且可导,则
(A)当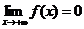 时,必有
时,必有 (B)当
(B)当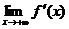 存在时,必有
存在时,必有
(C) 当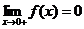 时,必有
时,必有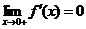 (D) 当
(D) 当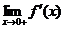 存在时,必有
存在时,必有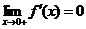 .
.
(4)设有三张不同平面,其方程为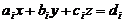 (
(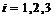 )它们所组成的线性方程组的系数矩阵与增广矩阵的秩都为2,则这三张平面可能的位置关系为
)它们所组成的线性方程组的系数矩阵与增广矩阵的秩都为2,则这三张平面可能的位置关系为

(5)设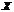 和
和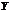 是相互独立的连续型随机变量,它们的密度函数分别为
是相互独立的连续型随机变量,它们的密度函数分别为 和
和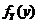 ,分布函数分别为
,分布函数分别为 和
和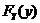 ,则
,则
(A) +
+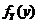 必为密度函数 (B)
必为密度函数 (B) 
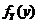 必为密度函数
必为密度函数
(C) +
+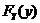 必为某一随机变量的分布函数 (D)
必为某一随机变量的分布函数 (D) 
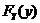 必为某一随机变量的分布函数.
必为某一随机变量的分布函数.
三、(本题满分6分)
设函数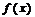 在
在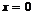 的某邻域具有一阶连续导数,且
的某邻域具有一阶连续导数,且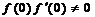 ,当
,当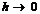 时,若
时,若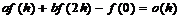 ,试求
,试求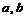 的值.
的值.
四、(本题满分7分)
已知两曲线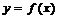 与
与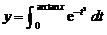 在点
在点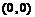 处的切线相同.求此切线的方程,并求极限
处的切线相同.求此切线的方程,并求极限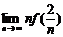 .
.
五、(本题满分7分)
计算二重积分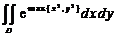 ,其中
,其中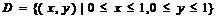 .
.
六、(本题满分8分)
设函数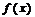 在
在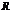 上具有一阶连续导数,
上具有一阶连续导数,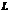 是上半平面(
是上半平面(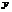 >0)内的有向分段光滑曲线,起点为(
>0)内的有向分段光滑曲线,起点为(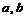 ),终点为(
),终点为( ).
).
记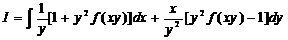 ,
,
(1)证明曲线积分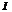 与路径
与路径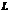 无关.
无关.
(2)当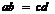 时,求
时,求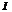 的值.
的值.
七、(本题满分7分)
(1)验证函数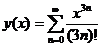 (
(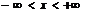 )满足微分方程
)满足微分方程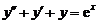 .
.
(2)求幂级数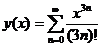 的和函数.
的和函数.
八、(本题满分7分)
设有一小山,取它的底面所在的平面为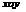 面,其底部所占的区域为
面,其底部所占的区域为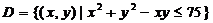 ,小山的高度函数为
,小山的高度函数为
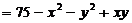 .
.
(1)设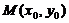 为区域
为区域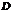 上一点,问
上一点,问 在该点沿平面上何方向的方向导数最大?若此方向的方向导数为
在该点沿平面上何方向的方向导数最大?若此方向的方向导数为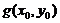 ,写出
,写出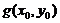 的表达式.
的表达式.
(2)现欲利用此小山开展攀岩活动,为此需要在山脚下寻找一山坡最大的点作为攀登的起点.也就是说要在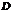 的边界线上找出使(1)中
的边界线上找出使(1)中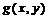 达到最大值的点.试确定攀登起点的位置.
达到最大值的点.试确定攀登起点的位置.
九、(本题满分6分)
已知四阶方阵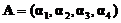 ,
, 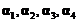 均为四维列向量,其中
均为四维列向量,其中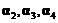 线性无关,
线性无关,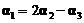 .若
.若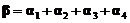 ,求线性方程组
,求线性方程组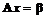 的通解.
的通解.
十、(本题满分8分)
设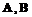 为同阶方阵,
为同阶方阵,
(1)若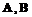 相似,证明
相似,证明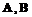 的特征多项式相等.
的特征多项式相等.
(2)举一个二阶方阵的例子说明(1)的逆命题不成立.
(3)当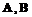 为实对称矩阵时,证明(1)的逆命题成立.
为实对称矩阵时,证明(1)的逆命题成立.
十一、(本题满分7分)
设维随机变量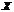 的概率密度为
的概率密度为

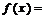
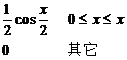 对
对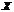 独立地重复观察4次,用
独立地重复观察4次,用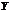 表示观察值大于
表示观察值大于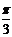 的次数,求
的次数,求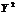 的数学期望.
的数学期望.
十二、(本题满分7分)
设总体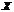 的概率分布为
的概率分布为
其中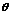 (
(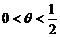 )是未知参数,利用总体
)是未知参数,利用总体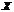 的如下样本值 3,1,3,0,3,1,2,3.
的如下样本值 3,1,3,0,3,1,2,3.
求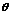 的矩估计和最大似然估计值.
的矩估计和最大似然估计值.
2002年考研数学一试题答案与解析
一、填空题
(1)【分析】 原式
(2)【分析】 方程两边对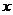 两次求导得
两次求导得
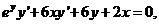 ①
①
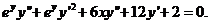 ②
②
以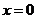 代入原方程得
代入原方程得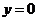 ,以
,以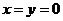 代入①得
代入①得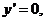 ,再以
,再以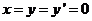 代入②得
代入②得
(3)【分析】 这是二阶的可降阶微分方程.
令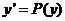 (以
(以 为自变量),则
为自变量),则
代入方程得  ,即
,即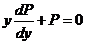 (或
(或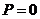 ,但其不满足初始条件
,但其不满足初始条件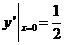 ).
).
分离变量得 
积分得 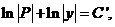 即
即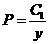 (
(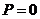 对应
对应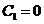 );
);
由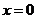 时
时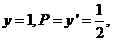 得
得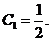 于是
于是
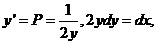 积分得
积分得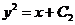 .
.
又由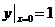 得
得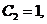 所求特解为
所求特解为
(4)【分析】 因为二次型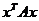 经正交变换化为标准型时,标准形中平方项的系数就是二次型矩阵
经正交变换化为标准型时,标准形中平方项的系数就是二次型矩阵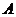 的特征值,所以
的特征值,所以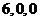 是
是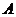 的特征值.
的特征值.
又因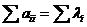 ,故
,故
(5)【分析】 设事件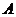 表示“二次方程
表示“二次方程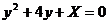 无实根”,则
无实根”,则
 依题意,有
依题意,有 
而 
即 
二、选择题
(1)【分析】 这是讨论函数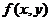 的连续性,可偏导性,可微性及偏导数的连续性之间的关系.我们知道,
的连续性,可偏导性,可微性及偏导数的连续性之间的关系.我们知道,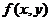 的两个偏导数连续是可微的充分条件,若
的两个偏导数连续是可微的充分条件,若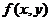 可微则必连续,故选(A).
可微则必连续,故选(A).
(2)【分析】 由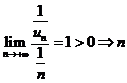 充分大时即
充分大时即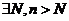 时
时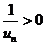 ,且
,且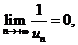 不妨认为
不妨认为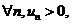 因而所考虑级数是交错级数,但不能保证
因而所考虑级数是交错级数,但不能保证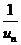 的单调性.
的单调性.
按定义考察部分和


 原级数收敛.
原级数收敛.
再考察取绝对值后的级数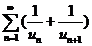 .注意
.注意
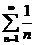 发散
发散
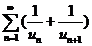 发散.因此选(C).
发散.因此选(C).
(3)【分析】 证明(B)对:反证法.假设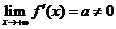 ,则由拉格朗日中值定理,
,则由拉格朗日中值定理,

(当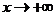 时,
时,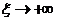 ,因为
,因为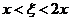 );但这与
);但这与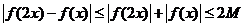 矛盾
矛盾
(4)【分析】 因为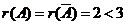 ,说明方程组有无穷多解,所以三个平面有公共交点且不唯一,因此应选(B).
,说明方程组有无穷多解,所以三个平面有公共交点且不唯一,因此应选(B).
(A)表示方程组有唯一解,其充要条件是
(C)中三个平面没有公共交点,即方程组无解,又因三个平面中任两个都不行,故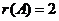 和
和
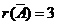 ,且
,且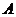 中任两个平行向量都线性无关.
中任两个平行向量都线性无关.
类似地,(D)中有两个平面平行,故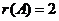 ,
,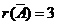 ,且
,且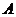 中有两个平行向量共线.
中有两个平行向量共线.
(5)【分析】 首先可以否定选项(A)与(C),因

对于选项(B),若 则对任何
则对任何
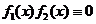 ,
,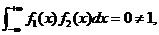 因此也应否定(C),综上分析,用排除法应选(D).
因此也应否定(C),综上分析,用排除法应选(D).
进一步分析可知,若令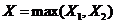 ,而
,而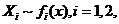 则
则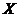 的分布函数
的分布函数 恰是
恰是


三、【解】 用洛必达法则.由题设条件知
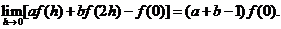 由于
由于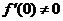 ,故必有
,故必有
又由洛必达法则 

及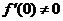 ,则有
,则有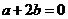 .
.
综上,得
四、【解】 由已知条件得


故所求切线方程为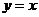 .由导数定义及数列极限与函数极限的关系可得
.由导数定义及数列极限与函数极限的关系可得

五、【分析与求解】 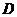 是正方形区域如图.因在
是正方形区域如图.因在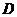 上被积函数分块表示
上被积函数分块表示
&n