|
微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
积分求面积A; 旋转体体积可用一大立体(圆锥)体积减去一小立体体积进行计算,为了帮助理解,可画一草图.
【详解】 (1) 设切点的横坐标为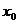 ,则曲线y=lnx在点 ,则曲线y=lnx在点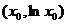 处的切线方程是 处的切线方程是
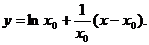
由该切线过原点知 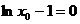 ,从而 ,从而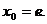 所以该切线的方程为 所以该切线的方程为
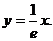
平面图形D的面积

(2) 切线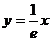 与x轴及直线x=e所围成的三角形绕直线x=e旋转所得的圆锥体积为 与x轴及直线x=e所围成的三角形绕直线x=e旋转所得的圆锥体积为 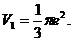
曲线y=lnx与x轴及直线x=e所围成的图形绕直线x=e旋转所得的旋转体体积为
 , ,
因此所求旋转体的体积为
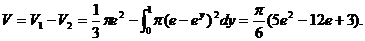
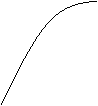
 y y
   1 1
  D D
 O 1 e x O 1 e x
【评注】 本题不是求绕坐标轴旋转的体积,因此不能直接套用现有公式. 也可考虑用微元法分析.
四 、(本题满分12分)
将函数 展开成x的幂级数,并求级数 展开成x的幂级数,并求级数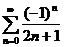 的和. 的和.
【分析】 幂级数展开有直接法与间接法,一般考查间接法展开,即通过适当的恒等变形、求导或积分等,转化为可利用已知幂级数展开的情形。本题可先求导,再利用函数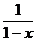
的幂级数展开 即可,然后取x为某特殊值,得所求级数的和. 即可,然后取x为某特殊值,得所求级数的和.
【详解】 因为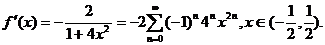
又f(0)= , 所以 , 所以
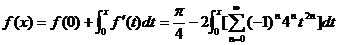
=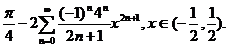
因为级数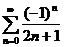 收敛,函数f(x)在 收敛,函数f(x)在 处连续,所以 处连续,所以

令 ,得 ,得
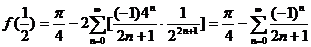 , ,
再由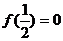 ,得 ,得
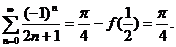
五 、(本题满分10分)
已知平面区域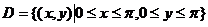 ,L为D的正向边界. 试证: ,L为D的正向边界. 试证:
(1) 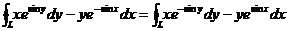 ; ;
(2) 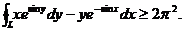
【分析】 本题边界曲线为折线段,可将曲线积分直接化为定积分证明,或曲线为封闭正向曲线,自然可想到用格林公式;(2)的证明应注意用(1)的结果.
【详解】 方法一:
(1) 左边=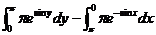
=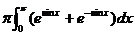 , ,
右边=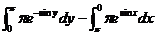
=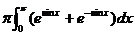 , ,
所以 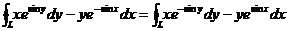 . .
(2) 由于 ,故由(1)得 ,故由(1)得
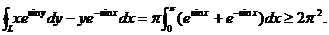
方法二:
(1) 根据格林公式,得
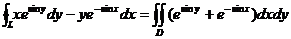 , ,
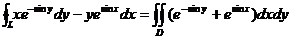 . .
因为D 具有轮换对称性,所以
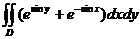 = =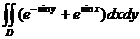 , ,
故 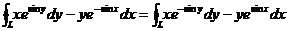 . .
(2) 由(1)知
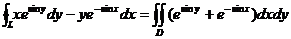
=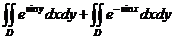
=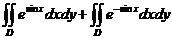 (利用轮换对称性) (利用轮换对称性)
=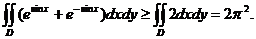
【评注】 本题方法一与方法二中的定积分与二重积分是很难直接计算出来的,因此期望通过计算出结果去证明恒等式与不等式是困难的. 另外,一个题由两部分构成时,求证第二部分时应首先想到利用第一部分的结果,事实上,第一部分往往是起桥梁作用的.
六 、(本题满分10分)
某建筑工程打地基时,需用汽锤将桩打进土层. 汽锤每次击打,都将克服土层对桩的阻力而作功. 设土层对桩的阻力的大小与桩被打进地下的深度成正比(比例系数为k,k>0).汽锤第一次击打将桩打进地下a m. 根据设计方案,要求汽锤每次击打桩时所作的功与前一次击打时所作的功之比为常数r(0<r<1). 问
(1) 汽锤击打桩3次后,可将桩打进地下多深?
(2) 若击打次数不限,汽锤至多能将桩打进地下多深?
(注:m表示长度单位米.)
【分析】 本题属变力做功问题,可用定积分进行计算,而击打次数不限,相当于求数列的极限.
【详解】 (1) 设第n次击打后,桩被打进地下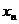 ,第n次击打时,汽锤所作的功为 ,第n次击打时,汽锤所作的功为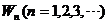 . 由题设,当桩被打进地下的深度为x时,土层对桩的阻力的大小为 . 由题设,当桩被打进地下的深度为x时,土层对桩的阻力的大小为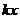 ,所以 ,所以
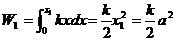 , ,
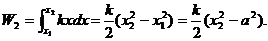
由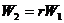 可得 可得
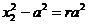
即 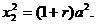
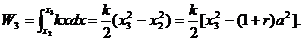
由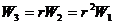 可得 可得
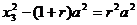 , ,
从而 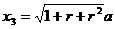 , ,
即汽锤击打3次后,可将桩打进地下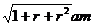 . .
(2) 由归纳法,设 ,则 ,则
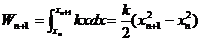
=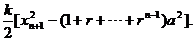
由于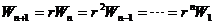 ,故得 ,故得
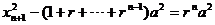 , ,
从而 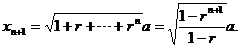
于是 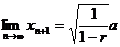 , ,
即若击打次数不限,汽锤至多能将桩打进地下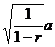 m. m.
【评注】 本题巧妙地将变力作功与数列极限两个知识点综合起来了,有一定难度。但用定积分求变力做功并不是什么新问题,何况本题的变力十分简单。
七 、(本题满分12分)
设函数y=y(x)在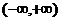 内具有二阶导数,且 内具有二阶导数,且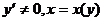 是y=y(x)的反函数. 是y=y(x)的反函数.
(1) 试将x=x(y)所满足的微分方程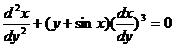 变换为y=y(x)满足的微分方程; 变换为y=y(x)满足的微分方程;
(2) 求变换后的微分方程满足初始条件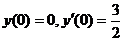 的解. 的解.
【分析】 将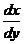 转化为 转化为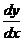 比较简单, 比较简单,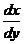 = =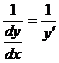 ,关键是应注意: ,关键是应注意:
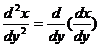 = =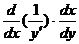
=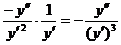 . .
然后再代入原方程化简即可.
【详解】 (1) 由反函数的求导公式知 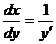 ,于是有 ,于是有
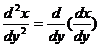 = =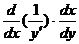 = =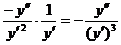 . .
代入原微分方程得
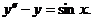 ( * ) ( * )
(2) 方程( * )所对应的齐次方程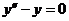 的通解为 的通解为

设方程( * )的特解为
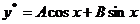 , ,
代入方程( * ),求得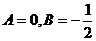 ,故 ,故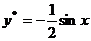 ,从而 ,从而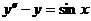 的通解是 的通解是
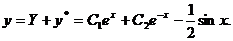
由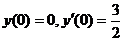 ,得 ,得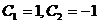 . 故所求初值问题的解为 . 故所求初值问题的解为
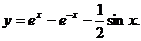
【评注】 本题的核心是第一步方程变换。
八 、(本题满分12分)
设函数f(x)连续且恒大于零,
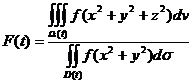 , ,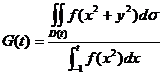 , ,
其中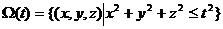 , ,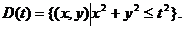
(1) 讨论F(t)在区间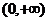 内的单调性. 内的单调性.
(2) 证明当t>0时,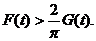
【分析】 (1) 先分别在球面坐标下计算分子的三重积分和在极坐标下计算分母的重积分,再根据导函数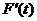 的符号确定单调性;(2) 将待证的不等式作适当的恒等变形后,构造辅助函数,再用单调性进行证明即可. 的符号确定单调性;(2) 将待证的不等式作适当的恒等变形后,构造辅助函数,再用单调性进行证明即可.
【详解】 (1) 因为
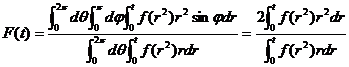 , ,
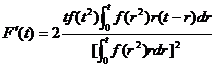 , ,
所以在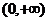 上 上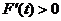 ,故F(t) 在 ,故F(t) 在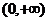 内单调增加. 内单调增加.
(2) 因
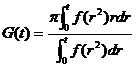 , ,
要证明t>0时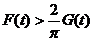 ,只需证明t>0时, ,只需证明t>0时,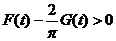 ,即 ,即
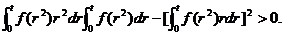
令 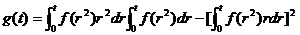 , ,
则 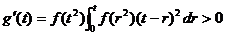 ,故g(t)在 ,故g(t)在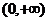 内单调增加. 内单调增加.
因为g(t)在t=0处连续,所以当t>0时,有g(t)>g(0).
又g(0)=0, 故当t>0时,g(t)>0,
因此,当t>0时,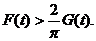
【评注】 本题将定积分、二重积分和三重积分等多个知识点结合起来了,但难点是证明(2)中的不等式,事实上,这里也可用柯西积分不等式证明:
|