微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
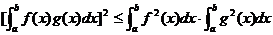 ,
,
在上式中取f(x)为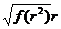 ,g(x)为
,g(x)为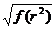 即可.
即可.
九 、(本题满分10分)
设矩阵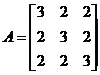 ,
,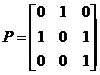 ,
,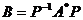 ,求B+2E的特征值与特征向量,其中
,求B+2E的特征值与特征向量,其中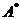 为A的伴随矩阵,E为3阶单位矩阵.
为A的伴随矩阵,E为3阶单位矩阵.
【分析】 可先求出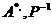 ,进而确定
,进而确定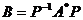 及B+2E,再按通常方法确定其特征值和特征向量;或先求出A的特征值与特征向量,再相应地确定A*的特征值与特征向量,最终根据B+2E与A*+2E相似求出其特征值与特征向量.
及B+2E,再按通常方法确定其特征值和特征向量;或先求出A的特征值与特征向量,再相应地确定A*的特征值与特征向量,最终根据B+2E与A*+2E相似求出其特征值与特征向量.
【详解】 方法一:
经计算可得
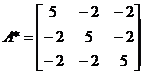 ,
,  ,
,
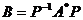 =
= .
.
从而
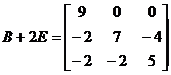 ,
,
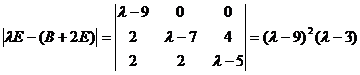 ,
,
故B+2E的特征值为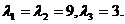
当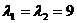 时,解
时,解 ,得线性无关的特征向量为
,得线性无关的特征向量为
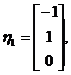
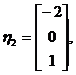
所以属于特征值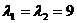 的所有特征向量为
的所有特征向量为
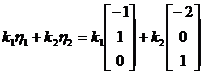 ,其中
,其中 是不全为零的任意常数.
是不全为零的任意常数.
当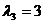 时,解
时,解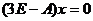 ,得线性无关的特征向量为
,得线性无关的特征向量为
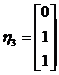 ,
,
所以属于特征值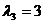 的所有特征向量为
的所有特征向量为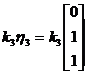 ,其中
,其中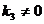 为任意常数.
为任意常数.
方法二:设A的特征值为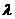 ,对应特征向量为
,对应特征向量为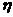 ,即
,即 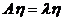 . 由于
. 由于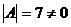 ,所以
,所以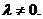
又因 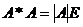 ,故有
,故有 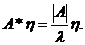
于是有 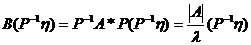 ,
,
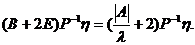
因此, 为B+2E的特征值,对应的特征向量为
为B+2E的特征值,对应的特征向量为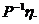
由于 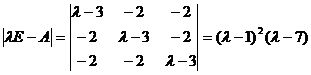 ,
,
故A的特征值为
当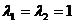 时,对应的线性无关特征向量可取为
时,对应的线性无关特征向量可取为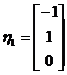 ,
, 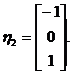
当 时,对应的一个特征向量为
时,对应的一个特征向量为
由  ,得
,得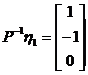 ,
, ,
,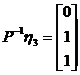 .
.
因此,B+2E的三个特征值分别为9,9,3.
对应于特征值9的全部特征向量为
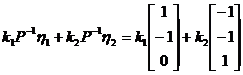 ,其中
,其中 是不全为零的任意常数;
是不全为零的任意常数;
对应于特征值3的全部特征向量为
 ,其中
,其中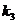 是不为零的任意常数.
是不为零的任意常数.
【评注】 设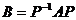 ,若
,若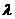 是A的特征值,对应特征向量为
是A的特征值,对应特征向量为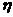 ,则B与A有相同的特征值,但对应特征向量不同,B对应特征值
,则B与A有相同的特征值,但对应特征向量不同,B对应特征值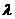 的特征向量为
的特征向量为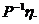
本题计算量大,但方法思路都是常规和熟悉的,主要是考查考生的计算能力。不过利用相似矩阵有相同的特征值以及A与A*的特征值之间的关系讨论,可适当降低计算量.
十 、(本题满分8分)
已知平面上三条不同直线的方程分别为

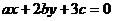 ,
,

 ,
,

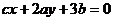 .
.
试证这三条直线交于一点的充分必要条件为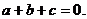
【分析】 三条直线相交于一点,相当于对应线性方程组有唯一解,进而转化为系数矩阵与增广矩阵的秩均为2.
【详解】 方法一:必要性
设三条直线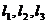 交于一点,则线性方程组
交于一点,则线性方程组
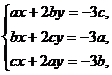 (*)
(*)
有唯一解,故系数矩阵 与增广矩阵
与增广矩阵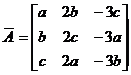 的秩均为2,于是
的秩均为2,于是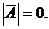
由于 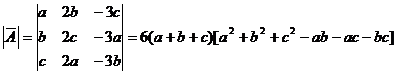
=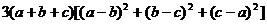 ,
,
但根据题设 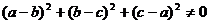 ,故
,故
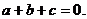
充分性:由 ,则从必要性的证明可知,
,则从必要性的证明可知,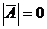 ,故秩
,故秩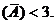
由于
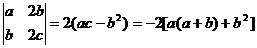
=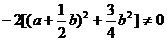 ,
,
故秩(A)=2. 于是,
秩(A)=秩 =2.
=2.
因此方程组(*)有唯一解,即三直线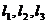 交于一点.
交于一点.
方法二:必要性
设三直线交于一点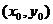 ,则
,则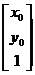 为Ax=0的非零解,其中
为Ax=0的非零解,其中
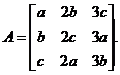
于是 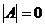 .
.
而 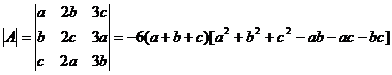
=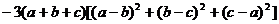 ,
,
但根据题设 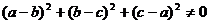 ,故
,故
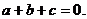
充分性:考虑线性方程组
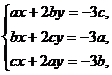 (*)
(*)
将方程组(*)的三个方程相加,并由a+b+c=0可知,方程组(*)等价于方程组
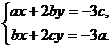 (* *)
(* *)
因为 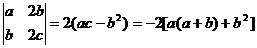
=-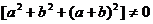 ,
,
故方程组(* *)有唯一解,所以方程组(*)有唯一解,即三直线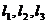 交于一点.
交于一点.
【评注】本题将三条直线的位置关系转化为方程组的解的判定,而解的判定问题又可转化为矩阵的秩计算,进而转化为行列式的计算,综合考查了多个知识点.
十一 、(本题满分10分)
已知甲、乙两箱中装有同种产品,其中甲箱中装有3件合格品和3件次品,乙箱中仅装有3件合格品. 从甲箱中任取3件产品放入乙箱后,求:
(1) 乙箱中次品件数的数学期望;
(2) 从乙箱中任取一件产品是次品的概率.
【分析】 乙箱中可能的次品件数为0,1,2,3,分别求出其概率,再按定义求数学期望即可;而求从乙箱中任取一件产品是次品的概率,涉及到两次试验,是典型的用全概率公式的情形,第一次试验的各种可能结果(取到的次品数)就是要找的完备事件组.
【详解】 (1) X的可能取值为0,1,2,3,X的概率分布为
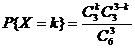 , k=0,1,2,3.
, k=0,1,2,3.
 即 X 0 1 2 3
即 X 0 1 2 3
 P
P 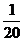
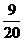
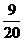
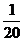
因此
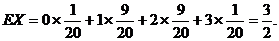
(2) 设A表示事件“从乙箱中任取一件产品是次品”,由于 ,
, ,
,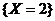 ,
, 构成完备事件组,因此根据全概率公式,有
构成完备事件组,因此根据全概率公式,有
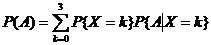
=
=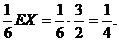
【评注】本题对数学期望的计算也可用分解法:
设

则 的概率分布为
的概率分布为

 0 1
0 1
 P
P 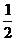
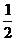
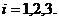
因为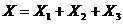 ,所以
,所以
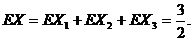
十二 、(本题满分8分)
设总体X的概率密度为
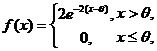
其中 是未知参数. 从总体X中抽取简单随机样本
是未知参数. 从总体X中抽取简单随机样本 ,记
,记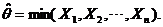
(1) 求总体X的分布函数F(x);
(2) 求统计量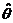 的分布函数
的分布函数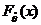 ;
;
(3) 如果用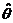 作为
作为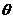 的估计量,讨论它是否具有无偏性.
的估计量,讨论它是否具有无偏性.
【分析】 求分布函数F(x)是基本题型;求统计量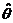 的分布函数
的分布函数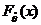 ,可作为多维相互独立且同分布的随机变量函数求分布函数,直接用定义即可;是否具有无偏性,只需检验
,可作为多维相互独立且同分布的随机变量函数求分布函数,直接用定义即可;是否具有无偏性,只需检验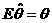 是否成立.
是否成立.
【详解】 (1)
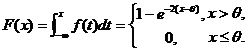
(2) 
=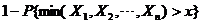
=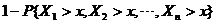
=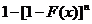
=
(3) 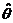 概率密度为
概率密度为
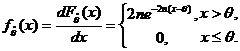
因为 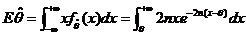
&n