微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
2003年全国硕士研究生入学统一考试
数学(一)试卷
一、填空题(本题共6小题,每小题4分,满分24分.把答案填在题中横线上)
(1)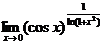 = .
= .
(2)曲面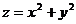 与平面
与平面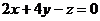 平行的切平面的方程是 .
平行的切平面的方程是 .
(3)设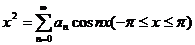 ,则
,则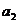 = .
= .
(4)从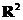 的基
的基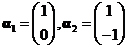 到基
到基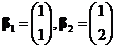 的过渡矩阵为 .
的过渡矩阵为 .
 (5)设二维随机变量
(5)设二维随机变量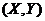 的概率密度为
的概率密度为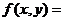
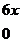
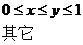 ,则
,则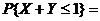 .
.
(6)已知一批零件的长度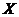 (单位:cm)服从正态分布
(单位:cm)服从正态分布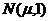 ,从中随机地抽取16个零件,得到长度的平均值为40 (cm),则
,从中随机地抽取16个零件,得到长度的平均值为40 (cm),则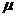 的置信度为0.95的置信区间是 .
的置信度为0.95的置信区间是 .
(注:标准正态分布函数值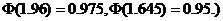
二、选择题(本题共6小题,每小题4分,满分24分.每小题给出的四个选项中,只有一个符合题目要求,把所选项前的字母填在题后的括号内)
|
(1)设函数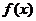 在 在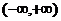 内连续,其导函数的图形如图所示,则 内连续,其导函数的图形如图所示,则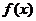 有 有
(A)一个极小值点和两个极大值点
(B)两个极小值点和一个极大值点
(C)两个极小值点和两个极大值点
(D)三个极小值点和一个极大值点
|
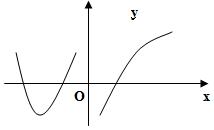
|
(2)设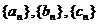 均为非负数列,且
均为非负数列,且 ,
,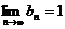 ,
,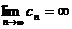 ,则必有
,则必有
(A)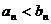 对任意
对任意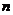 成立 (B)
成立 (B)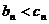 对任意
对任意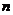 成立
成立
(C)极限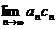 不存在 (D)极限
不存在 (D)极限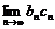 不存在
不存在
(3)已知函数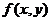 在点
在点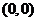 的某个邻域内连续,且
的某个邻域内连续,且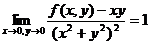 ,则
,则
(A)点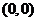 不是
不是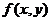 的极值点
的极值点
(B)点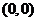 是
是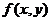 的极大值点
的极大值点
(C)点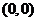 是
是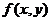 的极小值点
的极小值点
(D)根据所给条件无法判断点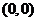 是否为
是否为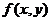 的极值点
的极值点
(4)设向量组I: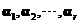 可由向量组II:
可由向量组II: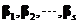 线性表示,则
线性表示,则
(A)当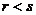 时,向量组II必线性相关 (B)当
时,向量组II必线性相关 (B)当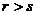 时,向量组II必线性相关
时,向量组II必线性相关
(C)当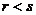 时,向量组I必线性相关 (D)当
时,向量组I必线性相关 (D)当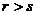 时,向量组I必线性相关
时,向量组I必线性相关
(5)设有齐次线性方程组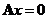 和
和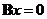 ,其中
,其中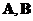 均为
均为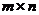 矩阵,现有4个命题:
矩阵,现有4个命题:
① 若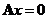 的解均是
的解均是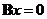 的解,则秩
的解,则秩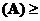 秩
秩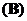
② 若秩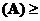 秩
秩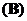 ,则
,则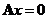 的解均是
的解均是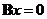 的解
的解
③ 若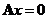 与
与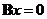 同解,则秩
同解,则秩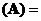 秩
秩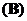
④ 若秩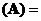 秩
秩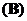 , 则
, 则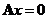 与
与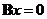 同解
同解
以上命题中正确的是
(A)①② (B)①③
(C)②④ (D)③④
(6)设随机变量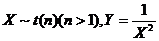 ,则
,则
(A)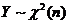 (B)
(B)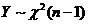
(C)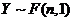 (D)
(D)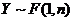
三、(本题满分10分)
过坐标原点作曲线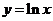 的切线,该切线与曲线
的切线,该切线与曲线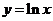 及
及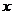 轴围成平面图形
轴围成平面图形 .
.
(1)求 的面积
的面积 .
.
(2)求 绕直线
绕直线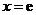 旋转一周所得旋转体的体积
旋转一周所得旋转体的体积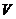 .
.
四、(本题满分12分)
将函数 展开成
展开成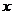 的幂级数,并求级数
的幂级数,并求级数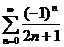 的和.
的和.
五 、(本题满分10分)
已知平面区域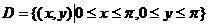 ,
,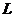 为
为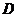 的正向边界.试证:
的正向边界.试证:
(1)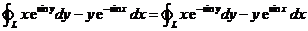 .
.
(2)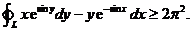
六 、(本题满分10分)
某建筑工程打地基时,需用汽锤将桩打进土层.汽锤每次击打,都将克服土层对桩的阻力而作功.设土层对桩的阻力的大小与桩被打进地下的深度成正比(比例系数为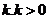 ).汽锤第一次击打将桩打进地下
).汽锤第一次击打将桩打进地下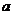 m.根据设计方案,要求汽锤每次击打桩时所作的功与前一次击打时所作的功之比为常数
m.根据设计方案,要求汽锤每次击打桩时所作的功与前一次击打时所作的功之比为常数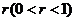 .问
.问
(1)汽锤击打桩3次后,可将桩打进地下多深?(2)若击打次数不限,汽锤至多能将桩打进地下多深?(注:m表示长度单位米.)
七 、(本题满分12分)
设函数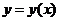 在
在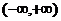 内具有二阶导数,且
内具有二阶导数,且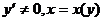 是
是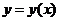 的反函数.
的反函数.
(1)试将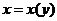 所满足的微分方程
所满足的微分方程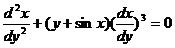 变换为
变换为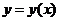 满足的微分方程.
满足的微分方程.
(2)求变换后的微分方程满足初始条件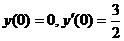 的解.
的解.
八 、(本题满分12分)
设函数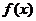 连续且恒大于零,
连续且恒大于零,
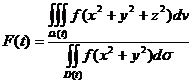 ,
,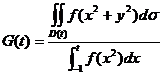 ,
,
其中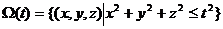 ,
,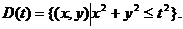
(1)讨论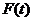 在区间
在区间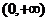 内的单调性.
内的单调性.
(2)证明当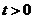 时,
时,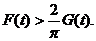
九 、(本题满分10分)
设矩阵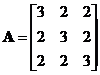 ,
,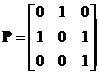 ,
,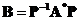 ,求
,求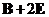 的特征值与特征向量,其中
的特征值与特征向量,其中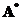 为
为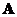 的伴随矩阵,
的伴随矩阵,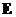 为3阶单位矩阵.
为3阶单位矩阵.
十 、(本题满分8分)
已知平面上三条不同直线的方程分别为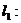
 ,
,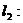
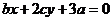 ,
,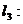
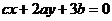 .试证这三条直线交于一点的充分必要条件为
.试证这三条直线交于一点的充分必要条件为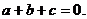
十一 、(本题满分10分)
已知甲、乙两箱中装有同种产品,其中甲箱中装有3件合格品和3件次品,乙箱中仅装有3件合格品. 从甲箱中任取3件产品放入乙箱后,求:
(1)乙箱中次品件数的数学期望.
(2)从乙箱中任取一件产品是次品的概率.
十二 、(本题满分8分)
设总体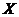 的概率密度为
的概率密度为

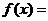
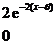
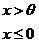
其中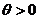 是未知参数. 从总体
是未知参数. 从总体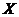 中抽取简单随机样本
中抽取简单随机样本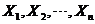 ,记
,记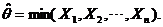
(1)求总体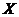 的分布函数
的分布函数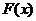 .(2)求统计量
.(2)求统计量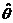 的分布函数
的分布函数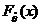 .(3)如果用
.(3)如果用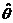 作为
作为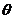 的估计量,讨论它是否具有无偏性.
的估计量,讨论它是否具有无偏性.
2003年硕士研究生入学考试(数学一)试题及答案解析
一、填空题(本题共6小题,每小题4分,满分24分. 把答案填在题中横线上)
(1) 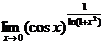 =
=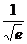 .
.
【分析】 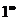 型未定式,化为指数函数或利用公式
型未定式,化为指数函数或利用公式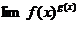
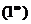 =
=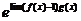 进行计算求极限均可.
进行计算求极限均可.
【详解1】 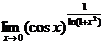 =
=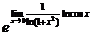 ,
,
而 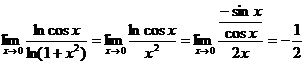 ,
,
故 原式=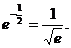
【详解2】 因为 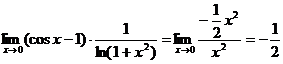 ,
,
所以 原式=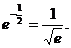
【评注】 本题属常规题型
(2) 曲面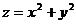 与平面
与平面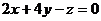 平行的切平面的方程是
平行的切平面的方程是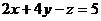 .
.
【分析】 待求平面的法矢量为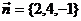 ,因此只需确定切点坐标即可求出平面方程, 而切点坐标可根据曲面
,因此只需确定切点坐标即可求出平面方程, 而切点坐标可根据曲面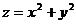 切平面的法矢量与
切平面的法矢量与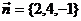 平行确定.
平行确定.
【详解】 令 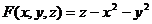 ,则
,则
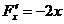 ,
,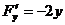 ,
, 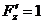 .
.
设切点坐标为 ,则切平面的法矢量为
,则切平面的法矢量为 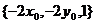 ,其与已知平面
,其与已知平面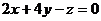 平行,因此有
平行,因此有
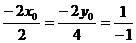 ,
,
可解得 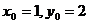 ,相应地有
,相应地有 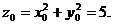
故所求的切平面方程为
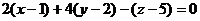 ,即
,即 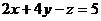 .
.
【评注】 本题属基本题型。
(3) 设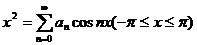 ,则
,则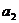 = 1 .
= 1 .
【分析】 将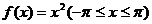 展开为余弦级数
展开为余弦级数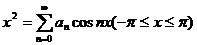 ,其系数计算公式为
,其系数计算公式为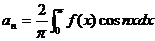 .
.
【详解】 根据余弦级数的定义,有
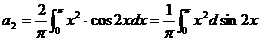
=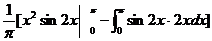
=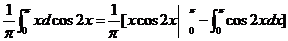
=1.
【评注】 本题属基本题型,主要考查傅里叶级数的展开公式,本质上转化为定积分的计算.
(4)从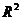 的基
的基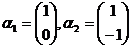 到基
到基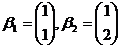 的过渡矩阵为
的过渡矩阵为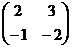 .
.
【分析】 n维向量空间中,从基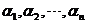 到基
到基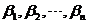 的过渡矩阵P满足
的过渡矩阵P满足
[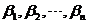 ]=[
]=[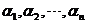 ]P,因此过渡矩阵P为:P=[
]P,因此过渡矩阵P为:P=[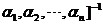 [
[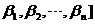 .
.
【详解】根据定义,从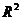 的基
的基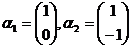 到基
到基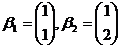 的过渡矩阵为
的过渡矩阵为
P=[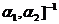 [
[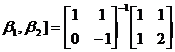 .
.
=
【评注】 本题属基本题型。
(5)设二维随机变量(X,Y)的概率密度为
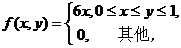
则
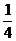 .
.
【分析】 已知二维随机变量(X,Y)的概率密度f(x,y),求满足一定条件的概率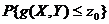 ,一般可转化为二重积分
,一般可转化为二重积分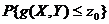 =
=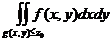 进行计算.
进行计算.
【详解】 由题设,有


=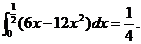
 y
y

 1
1


 D
D
 O
O 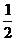 1 x
1 x
【评注】 本题属基本题型,但在计算二重积分时,应注意找出概率密度不为零与满足不等式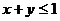 的公共部分D,再在其上积分即可. 完全类似例题见《文登数学全真模拟试卷》数学一P.14第一大题第(5)小题.
的公共部分D,再在其上积分即可. 完全类似例题见《文登数学全真模拟试卷》数学一P.14第一大题第(5)小题.
(6)已知一批零件的长度X (单位:cm)服从正态分布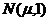 ,从中随机地抽取16个零件,得到长度的平均值为40 (cm),则
,从中随机地抽取16个零件,得到长度的平均值为40 (cm),则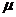 的置信度为0.95的置信区间是
的置信度为0.95的置信区间是 .
.
(注:标准正态分布函数值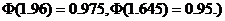
【分析】 已知方差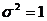 ,对正态总体的数学期望
,对正态总体的数学期望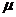 进行估计,可根据
进行估计,可根据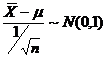 ,由
,由 确定临界值
确定临界值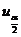 ,进而确定相应的置信区间.
,进而确定相应的置信区间.
【详解】 由题设,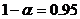 ,可见
,可见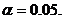 于是查标准正态分布表知
于是查标准正态分布表知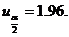 本题n=16,
本题n=16, 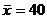 , 因此,根据
, 因此,根据 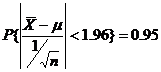 ,有
,有
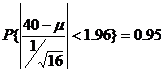 ,即
,即 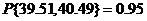 ,故
,故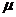 的置信度为0.9
的置信度为0.9