|
微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
; (B) 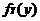
(C) 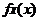 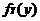 (D) (D)
二.填空题:11-16小题,每小题4分,共24分,请将答案写在答题纸指定位置上。
(11) 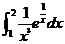 = =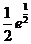 . .
(12)设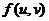 为二元可微函数, 为二元可微函数,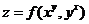 ,则 ,则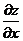 = =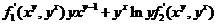 . .
(13)二阶常系数非齐次线性方程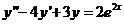 的通解为y= 的通解为y=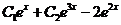 . .
(14)设曲面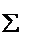 : :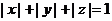 ,则 ,则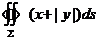 = =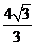 . .
(15)设矩阵A= ,则 ,则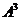 的秩为1. 的秩为1.
(16)在区间(0,1)中随机地取两个数,则这两个数之差的绝对值小于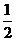 的概率为 的概率为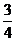 . .
三、解答题:17~24小题,共86分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤。

【详解】:
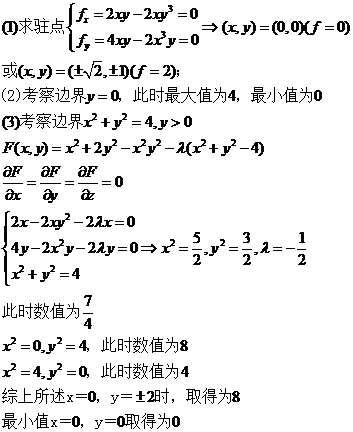
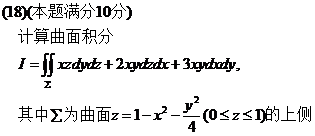
【详解】
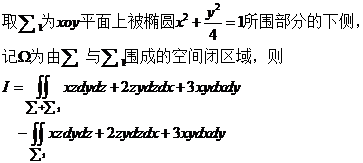
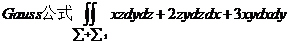 
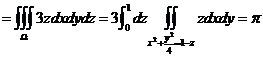
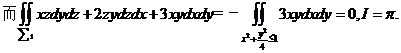
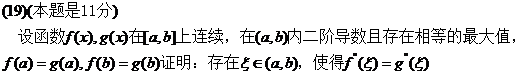
【详解】
证明:设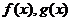 在 在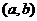 内某点 内某点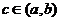 同时取得最大值,则 同时取得最大值,则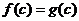 ,此时的c就是所求点 ,此时的c就是所求点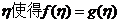 .若两个函数取得最大值的点不同则有设 .若两个函数取得最大值的点不同则有设
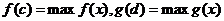 故有 故有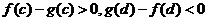 ,由介值定理,在 ,由介值定理,在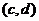 内肯定存在 内肯定存在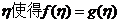 由罗尔定理在区间 由罗尔定理在区间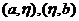 内分别存在一点 内分别存在一点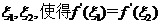 =0在区间 =0在区间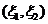 内再用罗尔定理,即 内再用罗尔定理,即
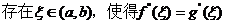
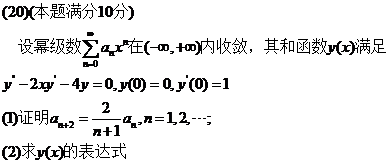
【详解】
(1) 将已知条件中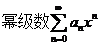 代入到微分方程中,整理即可得到: 代入到微分方程中,整理即可得到:
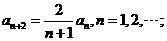
(2) 解题如下
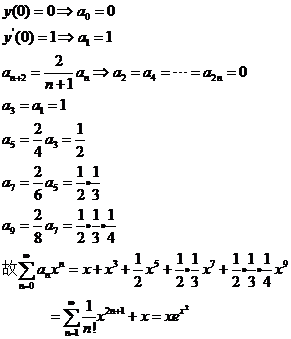
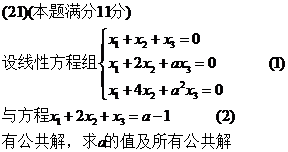
【详解】:
因为方程组(1)、(2)有公共解,即由方程组(1)、(2)组成的方程组
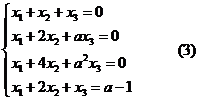 的解. 的解.
即距阵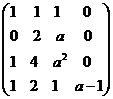 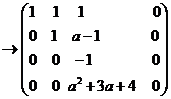 方程组(3)有解的充要条件为 方程组(3)有解的充要条件为
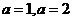 . .
当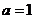 时,方程组(3)等价于方程组(1)即此时的公共解为方程组(1)的解.解方程组(1)的基础解系为 时,方程组(3)等价于方程组(1)即此时的公共解为方程组(1)的解.解方程组(1)的基础解系为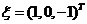 此时的公共解为: 此时的公共解为: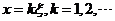
当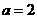 时,方程组(3)的系数距阵为 时,方程组(3)的系数距阵为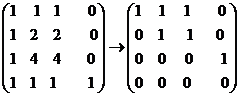 此时方程组(3)的解为 此时方程组(3)的解为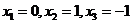 ,即公共解为: ,即公共解为: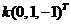
(22)设3阶对称矩阵A的特征向量值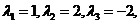 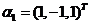 是A的属于 是A的属于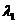 的一个特征向量,记 的一个特征向量,记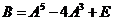 其中 其中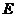 为3阶单位矩阵 为3阶单位矩阵
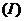 验证 验证 是矩阵 是矩阵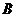 的特征向量,并求 的特征向量,并求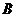 的全部特征值的特征向量; 的全部特征值的特征向量;
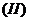 求矩阵 求矩阵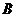 . .
【详解】:
(Ⅰ)可以很容易验证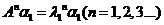 ,于是 ,于是
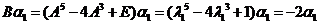
于是 是矩阵B的特征向量. 是矩阵B的特征向量.
B的特征值可以由A的特征值以及B与A的关系得到,即
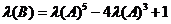 , ,
所以B的全部特征值为-2,1,1.
前面已经求得 为B的属于-2的特征值,而A为实对称矩阵, 为B的属于-2的特征值,而A为实对称矩阵,
于是根据B与A的关系可以知道B也是实对称矩阵,于是属于不同的特征值的特征向量正交,设B的属于1的特征向量为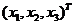 ,所以有方程如下: ,所以有方程如下:
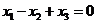
于是求得B的属于1的特征向量为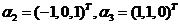
(Ⅱ)令矩阵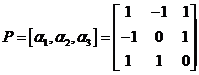 ,则 ,则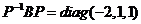 ,所以 ,所以
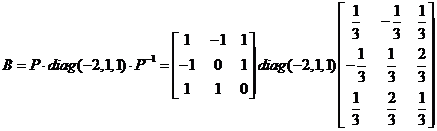
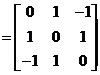
(23)设二维变量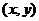 的概率密度为 的概率密度为
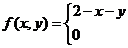 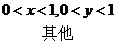
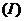 求 求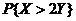 ; ;
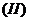 求 求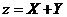 的概率密度. 的概率密度.
【详解】:
(Ⅰ)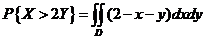 ,其中D为 ,其中D为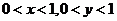 中 中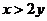 的那部分区域; 的那部分区域;
求此二重积分可得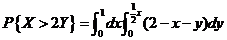
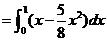

(Ⅱ)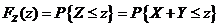
当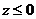 时, 时,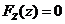 ; ;
当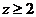 时, 时,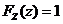 ; ;
当 时, 时,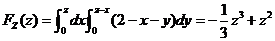
当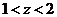 时, 时,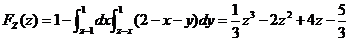
于是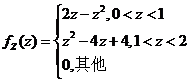
(24)设总体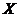 的概率密度为 的概率密度为
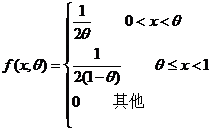
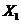 , ,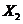 ,… ,…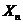 是来自总体 是来自总体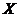 的简单随机样本, 的简单随机样本,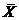 是样本均值 是样本均值
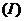 求参数 求参数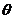 的矩估计量; 的矩估计量;
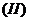 判断 判断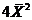 是否为 是否为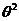 的无偏估计量,并说明理由. 的无偏估计量,并说明理由.
【详解】:
(Ⅰ)记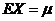 ,则 ,则
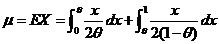
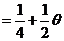 , ,
解出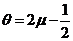 ,因此参数 ,因此参数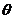 的矩估计量为 的矩估计量为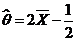 ; ;
(Ⅱ)只须验证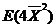 是否为 是否为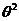 即可,而 即可,而
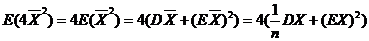 ,而 ,而
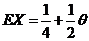 , ,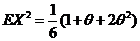 , ,
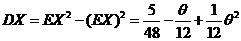 , ,
于是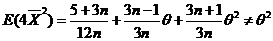
因此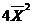 不是为 不是为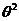 的无偏估计量. 的无偏估计量. |