|
微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
布函数为( )
 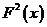 . .  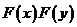 . .
 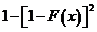 . .  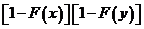 . .
解:选
分析;
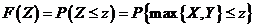 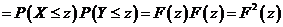
(8)设随机变量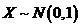 , ,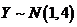 且相关系数 且相关系数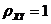 ,则( ) ,则( )
 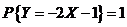 . .  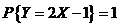 . .
 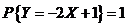 . .  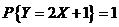 . .
解:选
分析:用排除法
设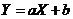 ,由 ,由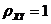 ,知道 ,知道 正相关,得 正相关,得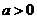 ,排除 ,排除 、 、
由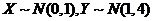 ,得 ,得
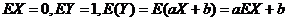
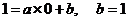
排除
故选择
二、填空题:9-14小题,每小题4分,共24分,请将答案写在答题纸指定位置上.
(9)微分方程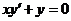 满足条件 满足条件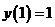 的解是 的解是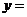  . .
解: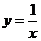
分析;由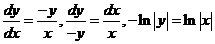 所以 所以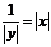 ,又 ,又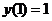 ,所以 ,所以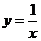 . .
(10)曲线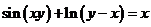 在点 在点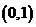 处的切线方程为 处的切线方程为 . .
解: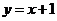 . .
分析:设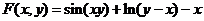 ,斜率 ,斜率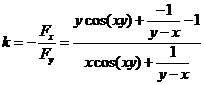 ,在 ,在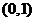 处, 处,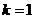 ,所以切线方程为 ,所以切线方程为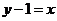 ,即 ,即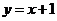
(11)已知幂级数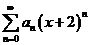 在 在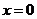 处收敛,在 处收敛,在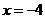 处发散,则幂级数 处发散,则幂级数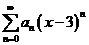 的收敛域为 的收敛域为 . .
解: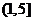 . .
分析:由题意知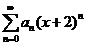 的收敛域为 的收敛域为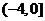 ,则 ,则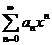 的收敛域为 的收敛域为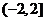 . .
所以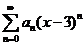 的收敛域为 的收敛域为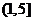 . .
(12)设曲面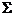 是 是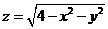 的上侧,则 的上侧,则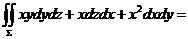  . .
解: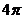
分析;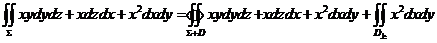
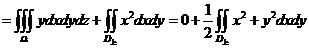
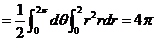
(13)设 为2阶矩阵, 为2阶矩阵,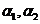 为线性无关的2维列向量, 为线性无关的2维列向量,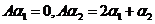 ,则 ,则 的非零特征值为 的非零特征值为 . .
解:1
分析: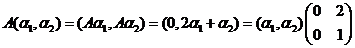
记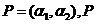 可逆,故 可逆,故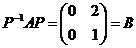
 与 与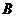 有相同的特征值 有相同的特征值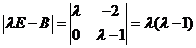 , ,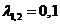 ,故非零的特征值为1。 ,故非零的特征值为1。
(14)设随机变量 服从参数为1的泊松分布,则 服从参数为1的泊松分布,则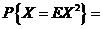  . .
解: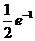
分析;因为 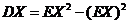 ,所以 ,所以 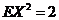 , , 服从参数为1的泊松分布, 服从参数为1的泊松分布,
所以 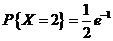
三、解答题:15-23小题,共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤.
(15)(本题满分10分)
求极限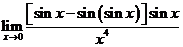
解: 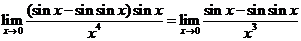 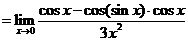
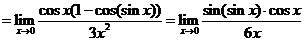
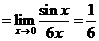
(16)(本题满分10分)
计算曲线积分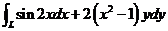 ,其中 ,其中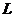 是曲线 是曲线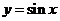 上从点 上从点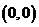 到点 到点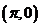 的一段. 的一段.
解: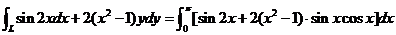
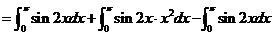
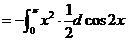
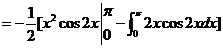
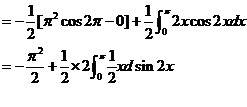
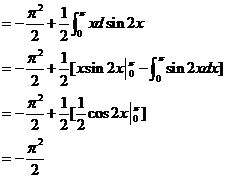
(17)(本题满分10分)
已知曲线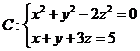 ,求曲线 ,求曲线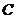 距离 距离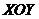 面最远的点和最近的点. 面最远的点和最近的点.
解: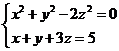
得: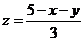
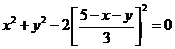
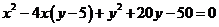
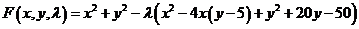
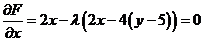
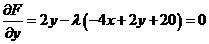
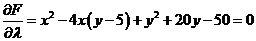
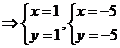
得: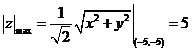
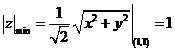 . .
(18)(本题满分10分)
函数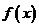 在 在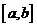 连续, 连续,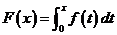 ,证明 ,证明 在 在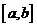 可导,且 可导,且
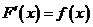 . .
证 :设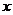 获得增量 获得增量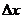 ,其绝对值足够小,使得 ,其绝对值足够小,使得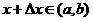 ,则 ,则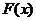 (如图,图中 (如图,图中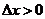 )在 )在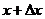 处的函数值为: 处的函数值为: 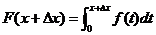
由此得函数的增量
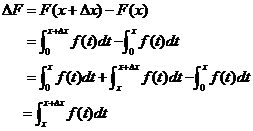
再应用积分中值定理,即有等式
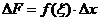
这里,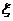 在 在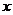 与 与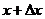 之间,把上式两端各除以 之间,把上式两端各除以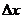 ,得函数增量与自变量的比值 ,得函数增量与自变量的比值
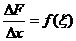
由于假设 连续,而 连续,而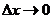 时, 时,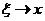 ,因此 ,因此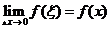 。于是,令 。于是,令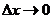 对上式两端取极限,左端的极限也应该等于 对上式两端取极限,左端的极限也应该等于 ,故 ,故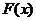 的导函数存在,并且 的导函数存在,并且
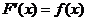
(19)(本题满分10分)
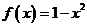 ,用余弦级数展开,并求 ,用余弦级数展开,并求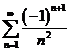 的和 的和
解:由 为偶函数,则 为偶函数,则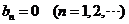
对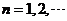
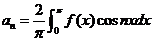
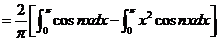
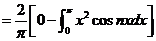
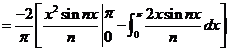
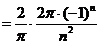
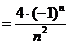
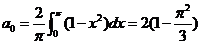
所以 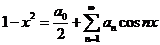
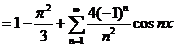
取 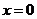 ,得 ,得 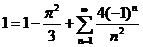
所以 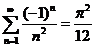
(20)(本题满分11分)
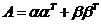 , ,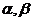 是三维列向量, 是三维列向量,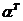 为 为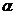 的转置, 的转置,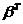 为 为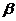 的转置 的转置
(1)证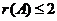 ;(2)若 ;(2)若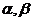 线性相关,则 线性相关,则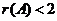 . .
解:①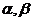 为三维列向量,则 为三维列向量,则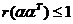 , ,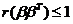
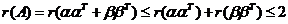
②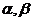 线性相关,不妨设 线性相关,不妨设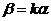 , ,
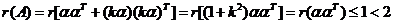
(21)(本题满分11分)
设矩阵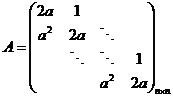 ,现矩阵 ,现矩阵 满足方程 满足方程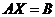 ,其中 ,其中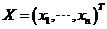 , ,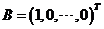 , ,
(1)求证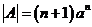
(2)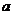 为何值,方程组有唯一解,求 为何值,方程组有唯一解,求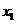
(3)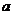 为何值,方程组有无穷多解,求通解 为何值,方程组有无穷多解,求通解
解:①
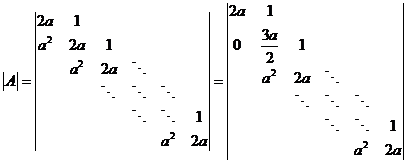
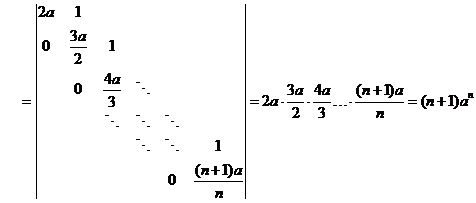
②方程组有唯一解
由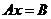 ,知 ,知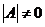 ,又 ,又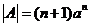 ,故 ,故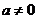 。 。
记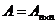 ,由克莱姆法则知, ,由克莱姆法则知,
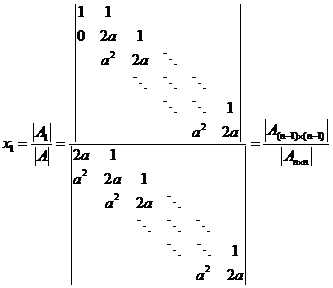
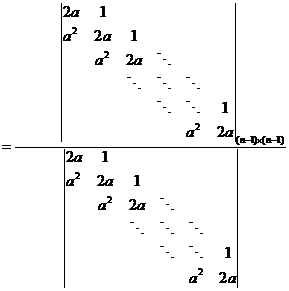 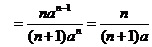
③方程组有无穷多解
由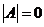 ,有 ,有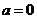 ,则 ,则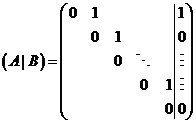 ,故 ,故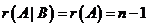
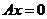 的同解方程组为 的同解方程组为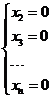 ,则基础解系为 ,则基础解系为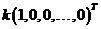 , ,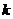 为任意常数。 为任意常数。
又
 ,故可取特解为 ,故可取特解为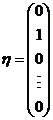
所以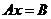 的通解为 的通解为 为任意常数。 为任意常数。
(22)(本题满分11分)
设随机变量 与 与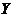 相互独立, 相互独立, 的概率分布为 的概率分布为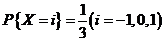 , ,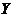 的概率密度为 的概率密度为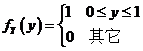 ,记 ,记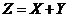
(1)求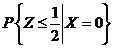
(2)求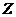 的概率密度. 的概率密度.
解:(1)
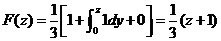
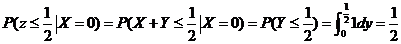
(2)当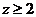 时, 时,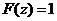
当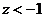 时, 时,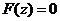
当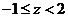 时, 时,
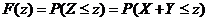
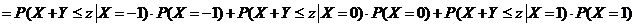 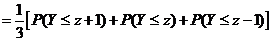
当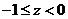 时, 时,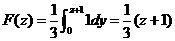
当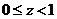 时, 时,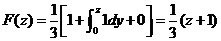
当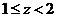 时, 时,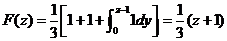
所以 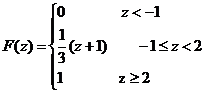 ,则 ,则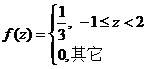
(23)(本题满分11分)
设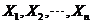 是总体为 是总体为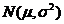 的简单随机样本.记 的简单随机样本.记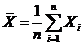 , ,
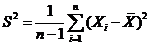 , ,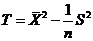
(1)证 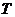 是 是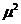 的无偏估计量. 的无偏估计量.
(2)当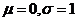 时 ,求 时 ,求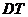 . .
解:(1)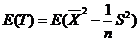  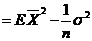
因为: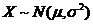 , , 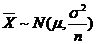 ,而 ,而 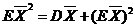 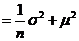
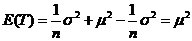 ,所以 T是 ,所以 T是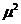 的无偏估计 的无偏估计
(2) 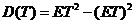 , ,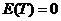 , , 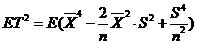
因为 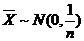 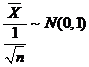
令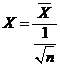 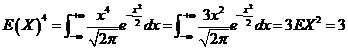
所以 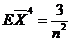
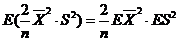 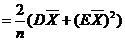
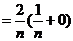 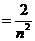
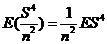
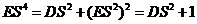
因为 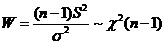 且 且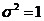
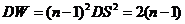
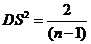 , ,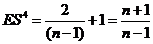
所以 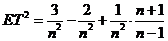 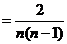
|