微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
nbsp; ②
又 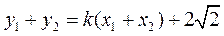 , ③
, ③
而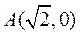 ,
,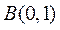 ,
,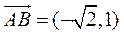 ,所以
,所以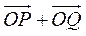 与
与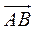 共线等价于
共线等价于
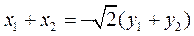 .
.
将②③代入上式,解得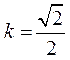 .
.
由(Ⅰ) 知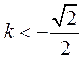 或
或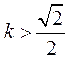 ,故没有符合题意的常数k.
,故没有符合题意的常数k.
10.(Ⅰ) 由椭圆定义知,
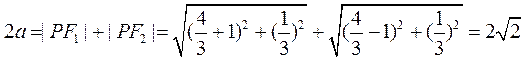 ,
,
所以 .
.
又由已知,c=1,
所以椭圆C的离心率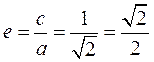 .
.
(Ⅱ) 由(Ⅰ) 知,椭圆C的方程为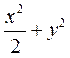 =1.
=1.
设点Q的坐标为(x,y).
(1) 当直线l与x轴垂直时,直线l与椭圆C交于(0,1),(0,-1)两点,
此时点Q的坐标为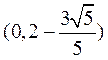 .
.
(2) 当直线l与x轴不垂直时,设直线l的方程为y=kx+2.
因为M,N在直线l上,可设点M,N的坐标分别为(x1, kx1+2),(x2,kx2+2),则
|AM|2=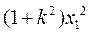 ,|AN|2=
,|AN|2=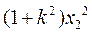 .
.
又 |AQ|2=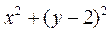 =
=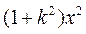 ,
,
由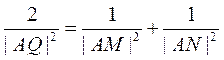 ,得
,得
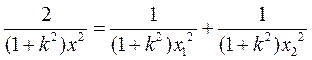 ,即
,即
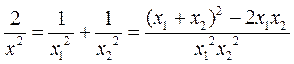 . ①
. ①
将y=kx+2代入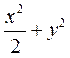 =1中,得
=1中,得
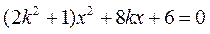 . ②
. ②
由△=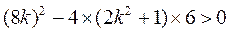 ,得
,得 .
.
由②可知,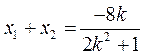 ,
,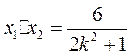 ,
,
代入①中并化简,得 x2=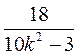 . ③
. ③
因为点Q在直线y=kx+2上,所以k=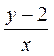 ,代入③中并化简,得
,代入③中并化简,得
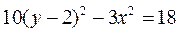 .
.
由③及k2>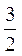 ,可知0<x2<
,可知0<x2<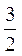 ,即
,即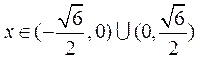 .
.
又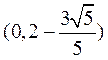 满足
满足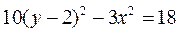 ,故
,故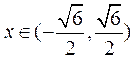 .
.
由题意,点Q(x,y)在椭圆C内,所以-1≤y≤1.
又由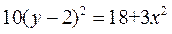 ,有
,有
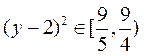 且-1≤y≤1,则
且-1≤y≤1,则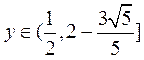 .
.
所以,点Q的轨迹方程为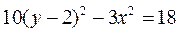 ,其中
,其中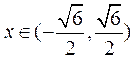 ,
,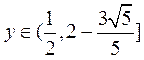 .
.
11.由已知得圆M的圆心为M(-1,0),半径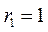 ;圆N的圆心为N(1,0),半径
;圆N的圆心为N(1,0),半径 .
.
设圆P的圆心为P(x,y),半径为R.
(Ⅰ) 因为圆P与圆M外切并且与圆N内切,所以
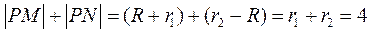 .
.
由椭圆的定义可知,曲线C是以M,N为左,右焦点,长半轴长为2,短半轴长为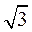 的椭圆(左顶点除外),其方程为
的椭圆(左顶点除外),其方程为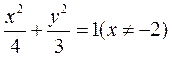 .
.
(Ⅱ) 对于曲线C上任意一点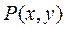 ,
,
由于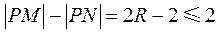 ,所以R
,所以R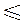 2,
2,
当且仅当圆P的圆心为(2,0)时,R=2,所以当圆P的半径最长时,
其方程为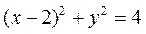 .
.
若l的倾斜角为90°,则l与y轴重合,可得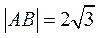 .
.
若l的倾斜角不为90°,则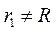 知l不平行于x轴,设l与x轴的交点为Q,
知l不平行于x轴,设l与x轴的交点为Q,
则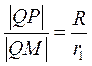 ,可求得Q(-4,0),所以可设l:y=k(x+4).由l与圆M相切
,可求得Q(-4,0),所以可设l:y=k(x+4).由l与圆M相切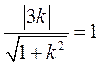 ,
,
解得k=±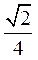 .
.
当k=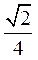 时,将y=
时,将y=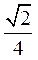 x+
x+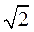 代入
代入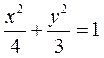 ,并整理得
,并整理得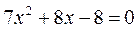 ,
,
解得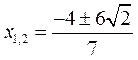 ,所以
,所以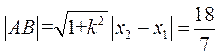 .
.
当k=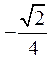 时,由图形的对称性可知,
时,由图形的对称性可知,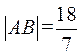 .
.
综上所述,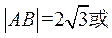
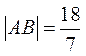 .
.
12.(Ⅰ) 由已知可得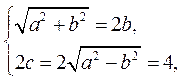
解得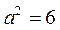 ,
,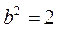 ,
,
所以椭圆C的标准方程是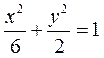 .
.
(Ⅱ) (ⅰ)由(Ⅰ)可得,F的坐标是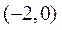 ,设T点的坐标为
,设T点的坐标为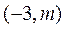 .
.
则直线TF的斜率kTF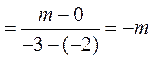 .
.
当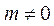 时,直线PQ的斜率kPQ
时,直线PQ的斜率kPQ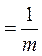 .直线PQ的方程是
.直线PQ的方程是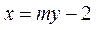 .
.
当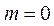 时,直线PQ的方程是
时,直线PQ的方程是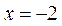 ,也符合
,也符合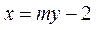 的形式.
的形式.
设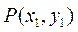 ,
,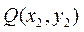 ,将直线PQ的方程与椭圆C的方程联立,得
,将直线PQ的方程与椭圆C的方程联立,得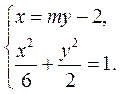
消去x,得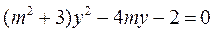 ,
,
其判别式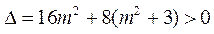 .
.
所以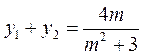 ,
,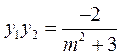 ,
,
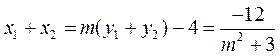 .
.
所以PQ的中点M的坐标为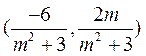 .
.
所以直线OM的斜率kOM 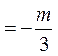 ,
,
又直线OT的斜率kOT 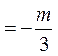 ,所以点M在直线OT上,
,所以点M在直线OT上,
因此OT平分线段PQ.
(ⅱ)由(ⅰ)可得,
|TF|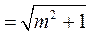 ,
,
|PQ|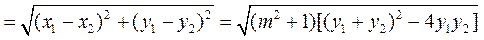
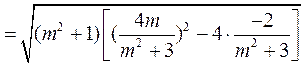
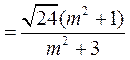 .
.
所以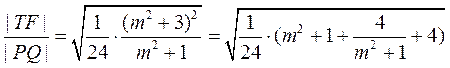 ≥
≥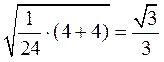 .
.
当且仅当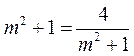 ,即
,即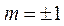 时,等号成立,此时
时,等号成立,此时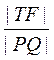 取得最小值.
取得最小值.
所以当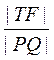 最小时,T点的坐标是
最小时,T点的坐标是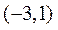 或
或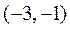 .
.
13.(Ⅰ) 对函数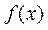 求导,可得
求导,可得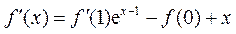 .
.
令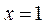 得
得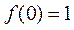 .
.
故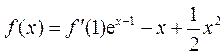 ,且有
,且有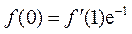 .
.
因此,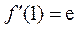 .
.
由此可得,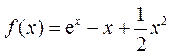 .
.
记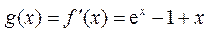 ,则
,则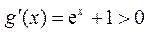 ,
,
所以 在
在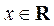 上单调递增.
上单调递增.
即当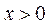 时,
时,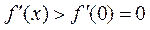 ;当
;当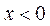 时,
时,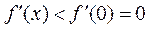 .
.
综上所述,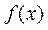 的解析式为
的解析式为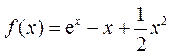 ,且单调递增区间为
,且单调递增区间为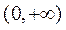 ,单调递减区间为
,单调递减区间为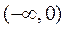 .
.
(Ⅱ) 记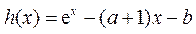 .
.
由已知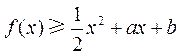 ,可得
,可得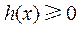 .
.
(1)当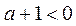 时,当
时,当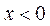 且
且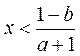 时,
时,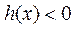 ,与
,与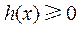 矛盾.
矛盾.
(2)当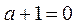 时,
时,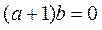 .
.
(3)当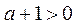 时,
时,
对 求导可得
求导可得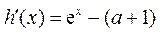 .
.
若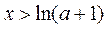 ,则
,则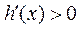 ;若
;若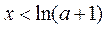 ,则
,则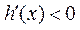 .
.
故当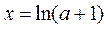 时,
时,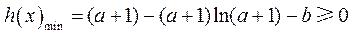 .
.
则有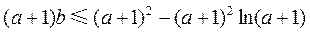 .
.
令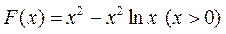 ,则
,则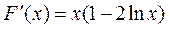 .
.
当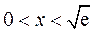 时,
时,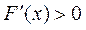 ;当
;当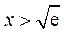 时,
时,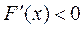 .
.
所以,当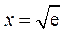 时,
时,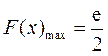 ;
;
从而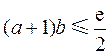 .
.
当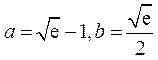 时,
时,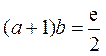 .
.
综上,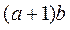 的最大值为
的最大值为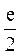 .
.
14.(Ⅰ) 函数f(x)的单调递减区间为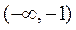 ,单调递增区间为
,单调递增区间为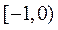 和
和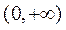 .
.
(Ⅱ) 由导数的几何意义可知,点A处的切线斜率为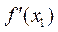 ,点B处的切线斜率为
,点B处的切线斜率为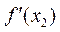 ,
,
故当点A处的切线与点B处的切线垂直时,有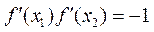 .
.
当x<0时,对函数f(x)求导,得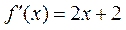 .
.
因为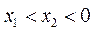 时, 所以
时, 所以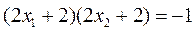 ,
,
所以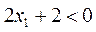 ,
,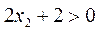 .
.
因此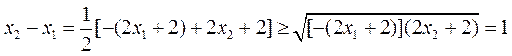 ,
,
当且仅当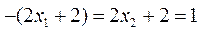 ,即
,即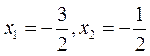 时等号成立.
时等号成立.
所以,函数f(x)的图象在点A,B处的切线互相垂直时,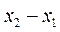 的最小值为1.
的最小值为1.
(Ⅲ) 当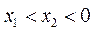 或
或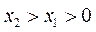 时,
时,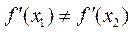 ,故
,故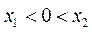 .
.
当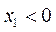 时,函数f(x)的图象在点
时,函数f(x)的图象在点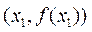 处的切线方程为
处的切线方程为
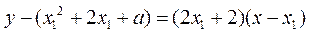 ,即
,即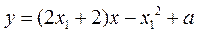 .
.
当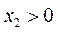 时,函数f(x)的图象在点
时,函数f(x)的图象在点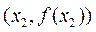 处的切线方程为
处的切线方程为
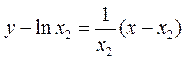 ,即
,即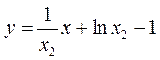 .
.
两切线重合的充要条件是
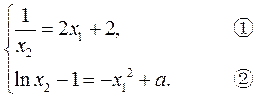
由①及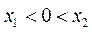 知,
知,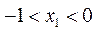 .
.
由①②得,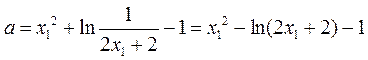 .
.
设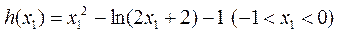 ,则
,则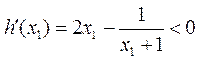 .
.
所以,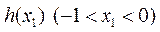 是减函数.
是减函数.
则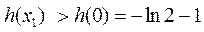 ,
,
所以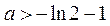 .
.
又当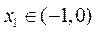 且趋近于-1时,
且趋近于-1时,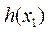 无限增大,
无限增大,
所以a的取值范围是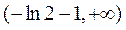 .
.
故当函数f(x)的图象在点A,B处的切线重合时,a的取值范围是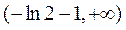 .
.
15.(Ⅰ) 由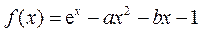 ,有
,有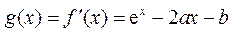 .
.
所以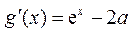 .
.
因此,当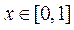 时,
时,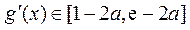 .
.
当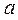 ≤
≤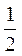 时,
时,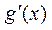 ≥0,所以
≥0,所以 在
在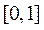 上单调递增,
上单调递增,
因此 在
在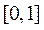 上的最小值是
上的最小值是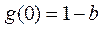 ;
;
当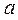 ≥
≥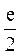 时,
时,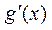 ≤0,所以
≤0,所以 在
在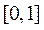 上单调递减,
上单调递减,
因此 在
在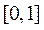 上的最小值是
上的最小值是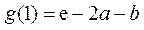 ;
;
当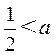 <
<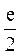 时,令
时,令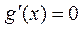 ,得
,得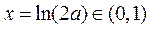 .
.
所以函数 在区间
在区间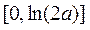 上单调递减,在区间
上单调递减,在区间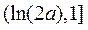 上单调递增.
上单调递增.
于是, 在
在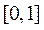 上的最小值是
上的最小值是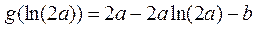 .
.
综上所述,当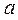 ≤
≤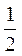 时,
时, 在
在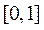 上的最小值是
上的最小值是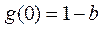 ;
;
当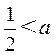 <
<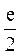 时,
时, 在
在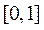 上的最小值是
上的最小值是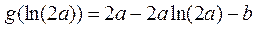 ;
;
当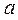 ≥
≥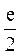 时,
时, 在
在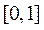 上的最小值是
上的最小值是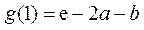 .
.
(Ⅱ) 设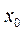 为
为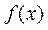 在区间(0,1)内的一个零点,则由
在区间(0,1)内的一个零点,则由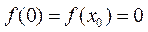 可知,
可知,
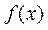 在区间
在区间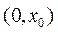 上不可能单调递增,也不可能单调递减.
上不可能单调递增,也不可能单调递减.
则 不可能恒为正,也不可能恒为负.
不可能恒为正,也不可能恒为负.
故 在区间
在区间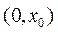 内存在零点
内存在零点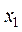 .
.
同理 在区间
在区间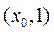 内存在零点
内存在零点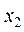 .
.
所以 在区间
在区间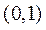 内至少有两个零点.
内至少有两个零点.
由(Ⅰ)知,当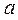 ≤
≤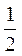 时,
时, 在
在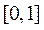 上单调递增,故
上单调递增,故 在
在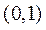 内至多有一个零点.
内至多有一个零点.
当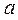 ≥
≥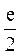 时,
时, 在
在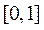 上单调递减,故
上单调递减,故 在
在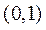 内至多有一个零点.
内至多有一个零点.
所以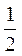 <
<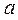 <
<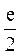 .
.
此时 在区间
在区间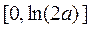 上单调递减,在区间
上单调递减,在区间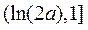 上单调递增.
上单调递增.
因此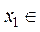
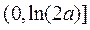 ,
,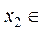
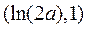 ,必有
,必有
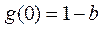 >0,
>0,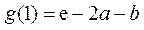 >0.
>0.
由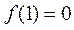 有
有 <2,有
<2,有
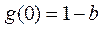
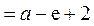 >0,
>0,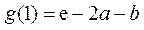
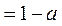 >0.
>0.
解得 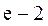 <
<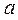 <1.
<1.
当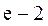 <
<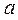 <1时,
<1时, 在区间
在区间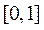 内有最小值
内有最小值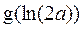 .
.
若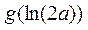 ≥0,则
≥0,则 ≥0(
≥0(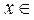
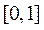 ),
),
从而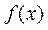 在区间
在区间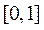 单调递增,这与
单调递增,这与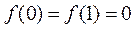 矛盾,所以
矛盾,所以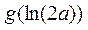 <0.
<0.
又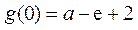 >0,
>0,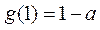 >0,
>0,
故此时 在
在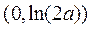 和
和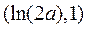 内各只有一个零点
内各只有一个零点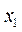 和
和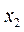 .
.
由此可知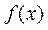 在
在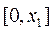 上单调递增,在
上单调递增,在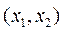 上单调递减,在
上单调递减,在 上单调递增.
上单调递增.
所以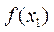 >
>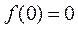 ,
,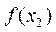 <
<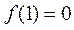 ,
,
故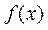 在
在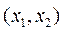 内有零点.
内有零点.
综上可知,a的取值范围是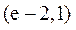 .
.
16.(Ⅰ) 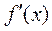 =
=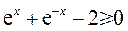 ,等号仅当
,等号仅当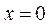 时成立.
时成立.
所以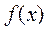 在
在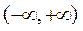 单调递增.
单调递增.
(Ⅱ) 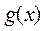 =
=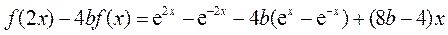 ,
,
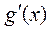 =
=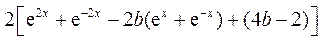 =
=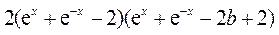 .
.
( i ) 当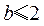 时,
时,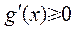 ,等号仅当
,等号仅当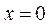 时成立,所以
时成立,所以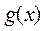 在
在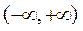 单调递增.而
单调递增.而 =0,所以对任意
=0,所以对任意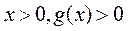 .
.
( ii ) 当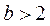 时,若
时,若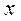 满足
满足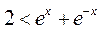
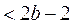 ,即
,即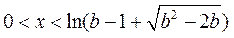 时,
时,
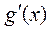 <0.而
<0.而 =0,因此当
=0,因此当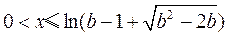 时,
时,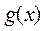 <0,不满足题意.
<0,不满足题意.
综上,b的最大值为2.
(Ⅲ) 由(Ⅱ)知,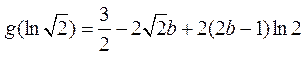 .
.
当b=2时,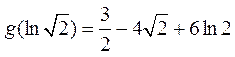 >0;
>0;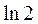 >
>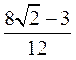 >0.6928;
>0.6928;
当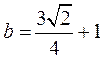 时,
时,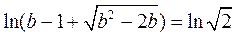 ,
,
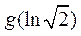 =
=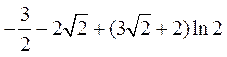 <0,
<0,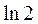 <
<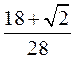 <0.6934.
<0.6934.
所以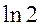 的近似值为0.693.
的近似值为0.693.
[①] 常见基本初等函数的导数公式:
(C为常数);,;;;
;;;.
[②] 公理1:如果一条直线上的两点在一个平面内,那么这条直线在此平面内.
公理2:过不在一条直线上的三点,有且只有一个平面.
公理3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.
公理4:平行于同一条直线的两条直线平行.
定 理:空间中如果两个角的两条边分别对应平行,那么这两个角相等或互补.