微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
1、简答题 如图所示,螺线管与相距L的两竖直放置的导轨相连,导轨处于垂直纸面向外、磁感应强度为B0的匀强磁场中.金属杆ab垂直导轨,杆与导轨接触良好,并可沿导轨无摩擦滑动.螺线管横截面积为S,线圈匝数为N,电阻为R1,管内有水平向左的变化磁场.已知金属杆ab的质量为m,电阻为R2,重力加速度为g.不计导轨的电阻,不计空气阻力,忽略螺线管磁场对杆ab的影响.
(1)为使ab杆保持静止,求通过ab的电流的大小和方向;
(2)当ab杆保持静止时,求螺线管内磁场的磁感应强度B的变化率;
(3)若螺线管内方向向左的磁场的磁感应强度的变化率
=k(k>0).将金属杆ab由静止释放,杆将向下运动.当杆的速度为v时,仍在向下做加速运动.求此时杆的加速度的大小.设导轨足够长.
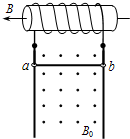
参考答案:(1)以ab为研究对象,根据平衡条件有mg=B0IL
解得:I=mgB0L
根据左手定则判断可知通过ab杆电流方向为由b到a.
(2)根据法拉第电磁感应定律得E=N△φ△t=NS△B△t
根据欧姆定律得I=ER1+R2
联立解得:△B△t=mg(R1+R2)B0LNS
(3)根据法拉第电磁感应定律 E1=NS△B△t=NSk
ab杆切割磁感线产生的电动势E2=B0Lv
总电动势E总=E1+E2
感应电流I′=E总R1+R2
根据牛顿第二定律mg-F=ma
安培力F=B0I′L
解得:a=g-B0L(NSk+B0Lv)m(R1+R2)
答:
(1)为使ab杆保持静止,通过ab的电流的大小为mgB0L,方向由b到a;
(2)当ab杆保持静止时,螺线管内磁场的磁感应强度B的变化率为△B△t=mg(R1+R2)B0LNS;
(3)此时杆的加速度的大小为g-B0L(NSk+B0Lv)m(R1+R2).
本题解析:
本题难度:一般
2、选择题 如图所示,两根足够长光滑平行金属导轨PQ、MN倾斜固定,倾角为θ=30°,相距为L,导轨处于磁感应强度为B、方向垂直导轨平面向下的匀强磁场中。有两根质量均为m的金属棒a、b,先将a棒垂直导轨放置,用跨过光滑定滑轮的细线与小球c连接,连接a棒的细线平行于导轨,由静止释放c,此后某时刻,将b棒也垂直导轨放置在导轨上,b刚好能静止。a棒在运动过程中始终与导轨垂直,两棒与导轨接触良好,导轨电阻不计,重力加速度为g。则
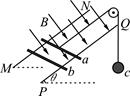
A.小球c的质量为m
B.b棒放上导轨前a棒的加速度为0.5g
C.b棒放上导轨后a棒中电流大小是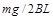
D.b棒放上导轨后,小球c减少的重力势能等于回路消耗的电能
参考答案:AC
本题解析:b棒静止说明b棒受力平衡,即安培力和重力沿斜面向下的分力平衡,此时a棒匀速向上运动,说明a棒受绳的拉力和重力沿斜面向下的分力大小以及沿斜面向下的安培力三个力平衡,c匀速下降,则c所受重力和绳的拉力大小平衡.由b平衡可知,安培力大小F安=mgsinθ,由a平衡可知F绳=F+mgsinθ=2mgsinθ,由c平衡可知F绳=mcg;因为绳中拉力大小相等,故2mgsinθ=mcg,即物块c的质量为2msinθ=m,故A正确;根据BIL= mgsin300,可知b棒放上导轨后a棒中电流大小是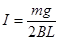 ,选项C正确;b棒放上导轨后,小球c减少的重力势能等于a增加的重力势能与回路消耗的电能之和,选项D错误;b棒放上导轨前a棒的加速度为
,选项C正确;b棒放上导轨后,小球c减少的重力势能等于a增加的重力势能与回路消耗的电能之和,选项D错误;b棒放上导轨前a棒的加速度为 =2ma,解得
=2ma,解得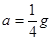 ,选项B错误;故选AC。
,选项B错误;故选AC。
考点:法拉第电磁感应定律;物体的平衡。
本题难度:困难
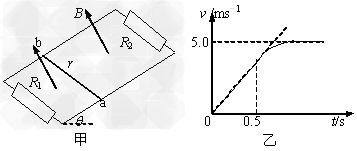
3、计算题 如图甲所示,两根足够长的光滑平行金属导轨相距为L=0.40m ,导轨平面与水平面成θ=30°角,上端和下端通过导线分别连接阻值R1=R2=1.2Ω的电阻,质量为m=0.20kg、阻值为r=0.20Ω的金属棒ab放在两导轨上,棒与导轨垂直且保持良好接触,整个装置处在垂直导轨平面向上的磁场中,取重力加速度g=10 m/s2。若所加磁场的磁感应强度大小 恒为B,通过小电动机对金属棒施加力,使金属棒沿导轨向上做匀加速直线运动,经过0.5s电动机的输出功率达到10W,此后保持电动机的输出功率不变,金属棒运动的v-t图如图乙所示。试求:
恒为B,通过小电动机对金属棒施加力,使金属棒沿导轨向上做匀加速直线运动,经过0.5s电动机的输出功率达到10W,此后保持电动机的输出功率不变,金属棒运动的v-t图如图乙所示。试求:
(1)磁感应强度B的大小;
(2)在0-0.5s时间内金属棒的加速度a的大小;
(3)在0-0.5s时间内电动机牵引力F与时间t的关系;
(4)如果在0-0.5 s时间内电阻R1产生的热量为0.135 J,则这段时间内电动机做的功。
参考答案:解:(1)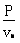 =mgsin30°+
=mgsin30°+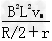 ,B=1 T
,B=1 T
(2) -mgsin30°-
-mgsin30°-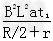 =ma ,a=
=ma ,a=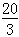 m/s2
m/s2
(3)F-mgsin30°- =ma ,F =
=ma ,F =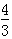 t+
t+ N
N
(4)Q1=(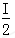 )2×1.2=0.3I2,Qr=0.2I2,Q总=2Q1+Qr=0.36 J
)2×1.2=0.3I2,Qr=0.2I2,Q总=2Q1+Qr=0.36 J
本题解析:
本题难度:一般
4、计算题 如图所示,有理想边界且范围足够大的两个水平匀强磁场I,Ⅱ,磁感应强度均为B,两水平边界间距为2L。有一质量为m、边长为L的正方形线框abcd由粗细均匀的导线制成,总电阻为R。线框从磁场I中某处由静止释放,运动过程中,线框平面始终在与磁场方向垂直的竖直平面内,且ab边平行于磁场边界。当ab 边刚离开磁场I时,线框恰好做匀速运动;当cd边进入磁场Ⅱ前,线框又做匀速运动。求:
(1)线框做匀速运动时,产生的感应电流的大小;
(2)线框从开始运动到完全进入磁场Ⅱ的过程中的最大速度;
(3)线框通过两磁场边界的整个过程中产生的焦耳热。

参考答案:解:(1)设线圈中的感应电流为I,则线圈做匀速运动时
BIL=mg
解得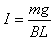
(2)设线圈做匀速运动的速度为v,产生的电动势为E,运动的最大速度为vm,则
E=BLv

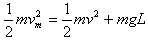
解得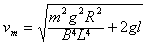
(3)由能量守恒定律可知,整个过程中产生的焦耳热Q=3mgL
本题解析:
本题难度:困难
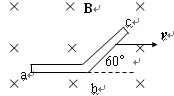
5、选择题 如图,abc为一金属导体,长ab =" bc" =" l" ,置于均匀磁场B中。当导体以速度v向右运动时,ac上产生的感应电动势为
A.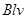
B.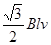
C.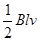
D.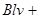
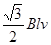
参考答案:B
本题解析:导体运动过程中,ab边不切割磁感线,bc边切割有效长度为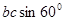 ,所以ac上产生的感应电动势为
,所以ac上产生的感应电动势为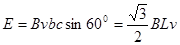
故选B
本题难度:一般